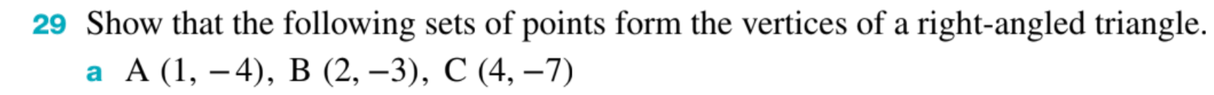SUMMARY
The discussion centers on demonstrating that a set of three points forms a right-angled triangle using both the Pythagorean theorem and slope calculations. The points (1, -4), (2, -3), and (4, -7) were analyzed, revealing that the slopes of segments AB and AC multiply to -1, confirming their perpendicularity. Additionally, the distances between the points were calculated, showing that the sum of the squares of the two shorter sides equals the square of the longest side, thus validating the right triangle condition.
PREREQUISITES
- Understanding of the Pythagorean theorem
- Knowledge of slope calculations in coordinate geometry
- Familiarity with distance formula in a Cartesian plane
- Basic vector operations and dot product
NEXT STEPS
- Study the Pythagorean theorem in-depth, including its applications in various geometrical contexts
- Learn about slope and its significance in determining perpendicular lines
- Explore the distance formula and its derivation from the Pythagorean theorem
- Investigate vector operations, particularly the dot product and its geometric interpretations
USEFUL FOR
Students and educators in mathematics, particularly those focusing on geometry and analytical methods, as well as anyone interested in understanding the properties of triangles and coordinate systems.