SUMMARY
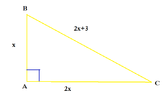
The discussion centers on solving the quadratic equation \(x^2 - 12x - 9 = 0\). Participants utilize the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) to derive the solutions. The final solutions are expressed as \(x = \frac{12 \pm 6\sqrt{5}}{2}\), which simplifies to approximately \(x = 12.72\). The conversation also touches on the application of the Pythagorean theorem in the context of the problem.
PREREQUISITES
- Understanding of quadratic equations and their solutions
- Familiarity with the quadratic formula
- Basic knowledge of the Pythagorean theorem
- Ability to simplify square roots and perform algebraic manipulations
NEXT STEPS
- Study the derivation and applications of the quadratic formula
- Learn about the properties of quadratic functions and their graphs
- Explore the Pythagorean theorem and its applications in geometry
- Practice solving various types of quadratic equations
USEFUL FOR
Students, educators, and anyone interested in mastering algebraic concepts, particularly those focused on quadratic equations and their solutions.