Showing That the Modified Bessel Function of the First Kind is a Solution

[womfalcs3]

Hello,

I am in the process of showing that the modified Bessel function, I_v(x), is a solution to the modified Bessel equation,

x^2*y''+x*y'-(x^2+v^2)*y=0

I have differentiated the MBF twice and plugged it into show that the left hand side is in fact 0.

After a good amount of work, I've come to the following left hand side:

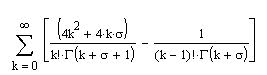
Where sigma=v.


Is that right? The math seems straight forward, and I only did one change of index that looks correct to me. I'm skeptical about the end result though.

 

[womfalcs3]

Sorry, the actual left hand side I have are those two terms inside the sum multiplied by (x/2)^2k+v.

All inside the sum.

 

[matematikawan]

Hello,

Is that right? The math seems straight forward, and I only did one change of index that looks correct to me. I'm skeptical about the end result though.

Not sure either. But the second term is undefined when k=0 , i.e. (-1)! = Γ(0) is undefined. Or do we assume the second term to be zero?

 

[womfalcs3]

Not sure either. But the second term is undefined when k=0 , i.e. (-1)! = Γ(0) is undefined. Or do we assume the second term to be zero?

Thank you for the response.

I just realized I made a mistake by changing the index, resulting in that denomintor. I eventually obtained a series that converged to 0.

Thank you again.