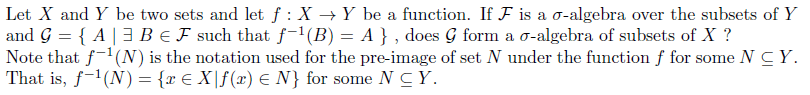Arenholt
- 9
- 0
Hi everyone, didn't know where to post question on sigma algebra so here it is:-
View attachment 5671
What I've tried till now:
Let $$C\in G$$
1) For $$C=X, f^{-1}(B)=X$$ which will be true for $$B=Y$$ (by definition)
2) For closure under complementation, to show $$C^{c}\in G. So, C^{c}=X\setminus C=X\setminus f^{-1}(B)=f^{-1}(Y)\setminus f^{-1}(B).$$
Can someone suggest how to proceed from here in order to show that the set G is closed under complementation? And how to prove the third property of Countable unions of subsets of X lying in G?
Thanks
View attachment 5671
What I've tried till now:
Let $$C\in G$$
1) For $$C=X, f^{-1}(B)=X$$ which will be true for $$B=Y$$ (by definition)
2) For closure under complementation, to show $$C^{c}\in G. So, C^{c}=X\setminus C=X\setminus f^{-1}(B)=f^{-1}(Y)\setminus f^{-1}(B).$$
Can someone suggest how to proceed from here in order to show that the set G is closed under complementation? And how to prove the third property of Countable unions of subsets of X lying in G?
Thanks
Attachments
Last edited: