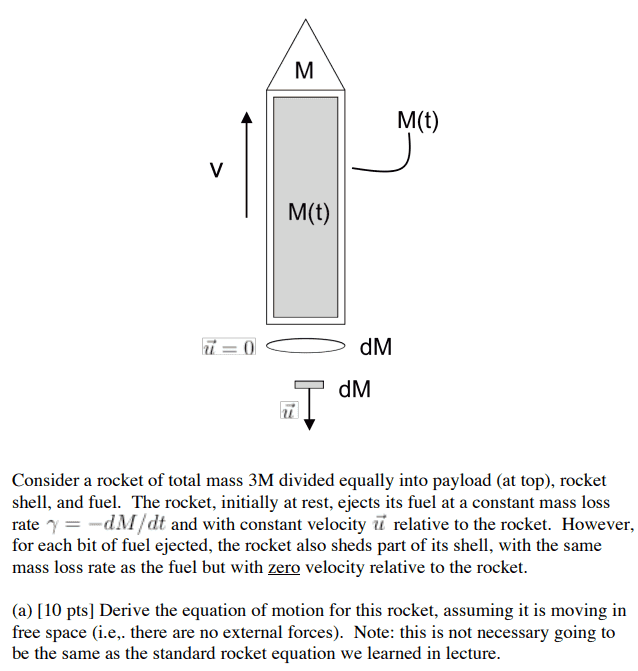
SUMMARY
The discussion centers on the rocket equation, specifically the relationship between the mass ejected by the rocket (##\Delta m##) and the change in the mass of the rocket (##\Delta M##). Participants clarify that ##\Delta m = -\Delta M## is correct because the rocket loses mass while ejecting fuel, which must be represented as equal and opposite quantities. The analogy of two glasses of water is used to illustrate that a decrease in mass in one context corresponds to an increase in another, reinforcing the necessity of the negative sign in the equation.
PREREQUISITES
- Understanding of the rocket equation and its components
- Familiarity with momentum conservation principles
- Basic knowledge of mass flow in physics
- Ability to interpret mathematical notation in physics
NEXT STEPS
- Study the derivation of the rocket equation in detail
- Explore momentum conservation in variable mass systems
- Learn about the implications of mass ejection on rocket propulsion
- Investigate vector notation in physics for clearer momentum representation
USEFUL FOR
Students of physics, aerospace engineers, and anyone interested in understanding the dynamics of rocket propulsion and mass flow in variable systems.