Simple Economic / Stock price model

[trollcast]

I'm trying to program a simple game with a handful of fictious companies on a virtual stock exchange that is semi realistic with price variations and trends over time.

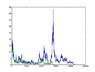
However I made a quick test using random functions and probabilities to produce the variations but I can't seem to strike a balance between stability (then the price just stays fairly constant and doesn't vary much) or instability where the price goes crazy.

Now its definitely a programming error but instead of guessing at what I need to change to get it to work I was wondering if there were any simple formulae or something that would be adequate to get a semi realistic price variation in the program?

 

[DavidHume]

You might want to pick, e.g. daily returns from a standard normal distribution, then apply these to a random starting price to generate realistic-looking returns. To make the returns more like actual market returns, you should alter the standard normal distribution to one with a skinnier bell and fatter tails.

 

[Tosh5457]

Use Cauchy distribution for the returns with a scale (gamma) of 1.7, it's the distribution Benoit Mandelbrot suggests.

By the way, will you simulate the volumes as well? I'd be very interested to see your program if you put it with volumes, since I guess then many differences will appear between the modeled prices and volumes and real ones.

 

[trollcast]

Use Cauchy distribution for the returns with a scale (gamma) of 1.7, it's the distribution Benoit Mandelbrot suggests.

By the way, will you simulate the volumes as well? I'd be very interested to see your program if you put it with volumes, since I guess then many differences will appear between the modeled prices and volumes and real ones.

How I'm planning to model it is:

I'm creating a class called Company that has a shareprice, buyprice and sellprice (I was going to just work out the buy and sell by going say 1% above for the buy and 1% below the shareprice for sell.

So the program will create a couple of instances of Company and set them a share price.

Now I want to work out how is the best way to move the shareprice on each time step to simulate how share prices vary in real life.

Not sure how I could include volumes into that simplistic model, maybe if I set each company a fixed number of shares?

 

[Tosh5457]

Not sure how I could include volumes into that simplistic model, maybe if I set each company a fixed number of shares?

Yes, and if you want it more realistically, put a small chance (like 0.001%) in each timestep that the numbers of share duplicate. I don't know how to model volumes though, I never looked at their distribution...

 

[BWV]

The standard methodology is log normal returns/ geometric Brownian motion

http://en.wikipedia.org/wiki/Geometric_Brownian_motion

No one really uses levy stable distributions as the fat tails have an auto correlating component. Stochastic, trending volatility such as GARCH is most typically uemployed

 

[trollcast]

I think I'll keep updating this thread to show the progress I'm making with this.

Just playing around with a random uniform distribution to start with has produced some quite good trends but its not very consistent:

eg.

But the prices are far too volatile and well random to be honest, also there's quite a few runs of it that doesn't produce a good trend as the price just tends to zero.

Its just a quick mock up in python with matplotlib and the 2 different libs just represent 2 different runs of the generator.

 

[NegativeDept]

The standard methodology is log normal returns/ geometric Brownian motion

http://en.wikipedia.org/wiki/Geometric_Brownian_motion

No one really uses levy stable distributions as the fat tails have an auto correlating component. Stochastic, trending volatility such as GARCH is most typically uemployed

I took a graduate financial modeling class, and it was just as BWV said. Geometric Brownian motion is known to be an imperfect model of real stocks, but it's a good start. It's also the model used to derive the famous Black-Scholes equation.

If you want to write your own stochastic numerical solver, consider the Euler-Maruyama method. It's based on the Euler method for numerical integration. It has similar properties, too - it's relatively intuitive and easy to code, but its accuracy and stability are pretty bad.

 

[Tosh5457]

I know the standard practice is using the normal distribution for the returns, but extreme movements are much much rarer in that case that in reality. In an era where we can use powerful computing and our knowledge of Mathematics is vast, I don't see the point in insisting of using a wrong model. The only reason it's still used for option valuation it's because of the properties of the normal distribution, that others don't have, such as finite variance.
Indeed the autocorrelation of the fat tails is a problem about using Cauchy distribution, but you could introduce that autocorrelation when extreme movements happen.