docnet
- 796
- 486
- Homework Statement
- what is the perimeter of the triangle ABC?
- Relevant Equations
- ##\angle A+\angle B + \angle C = \pi##
Hello, so I saw this problem on a website while looking up trigonometric identities and trying to solve it.
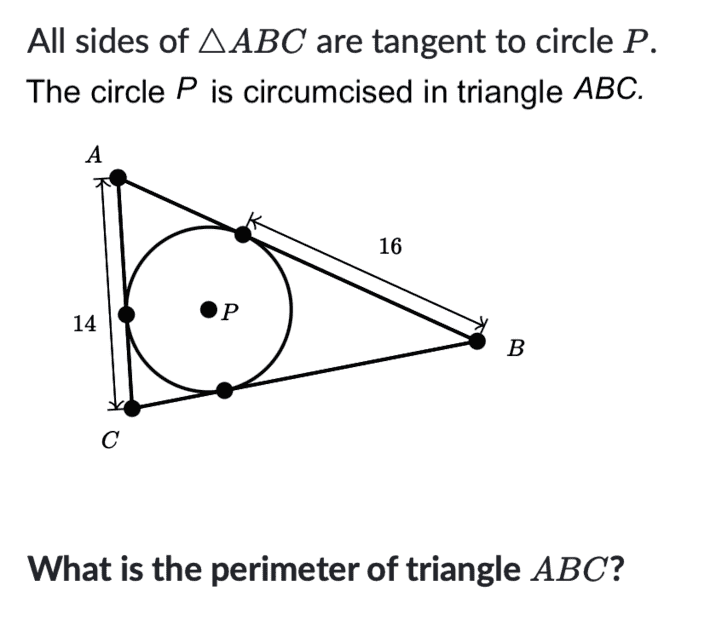
what I know:
The internal angles add up to pi
Let the tangent point between A and B be X
Let the tangent point between B and C be Y
Let the tangent point between C and A be Z
## \overline {AC} = 14##
## \overline {BX} = 16##Things I suspect are true, but have yet to prove:
##\overline {AX} =\overline {AZ}##
##\overline {CZ} =\overline {CY}##
##\overline {BX} =\overline {BY}##
Relations:
##\overline {CY}=14-\overline {AZ}##
##\overline {AX}=\overline {AB}-16##so far I only found three unknowns and only two equations! I think that this is strangely difficult.
what I know:
The internal angles add up to pi
Let the tangent point between A and B be X
Let the tangent point between B and C be Y
Let the tangent point between C and A be Z
## \overline {AC} = 14##
## \overline {BX} = 16##Things I suspect are true, but have yet to prove:
##\overline {AX} =\overline {AZ}##
##\overline {CZ} =\overline {CY}##
##\overline {BX} =\overline {BY}##
Relations:
##\overline {CY}=14-\overline {AZ}##
##\overline {AX}=\overline {AB}-16##so far I only found three unknowns and only two equations! I think that this is strangely difficult.