Smolyak reduced grid for three dimensions

[Frank Einstein]

Hello everyone. I am dealing with a stochastic optimization problem with three sources of uncertainty and I am using generalized polynomial chaos to solve this problem. The level with I am working is 1 (l=1). There are 3^3=27 realizations to make. I want to use instead a Smolyak reduced grid since in the future I will have to deal with more dimensions. My sources are the following: https://web.stanford.edu/~paulcon/slides/Oxford_2012.pdf and https://www.sciencedirect.com/science/article/pii/S0021999116301516.

My problem is as follows: The material says that the points which should be used and their weight can be described the following way:

(LaTex notation)
$A(l, d)= \sum_{l+1 \leq |i| \leq l+1} (-1)^{l+d-|i|} {d-1 \choose l+d-|i|}(U^{i_1} \otimes ... \otimes U^{i_d})

(Regular notation)
∑_{(l+1≤|i|≤l+d)} (-1)^(l+d-|i|) (d-1 l+d-|i|)(U^i₁⊗...⊗U^i_d)

Where d is the number of random variables, 3, l is the level, 1, |i| is the graded lexicographic order, (U^i₁⊗...⊗U^i_d) are the tensor product of the nodes for each dimension and (d-1 l+d-|i|) is a binomial coefficient.

Also, μ=f(ξ⁽¹⁾ξ⁽²⁾)°(ω), which means that the mean of the process is equal to the sum of all the realizations multiplied by their weight.

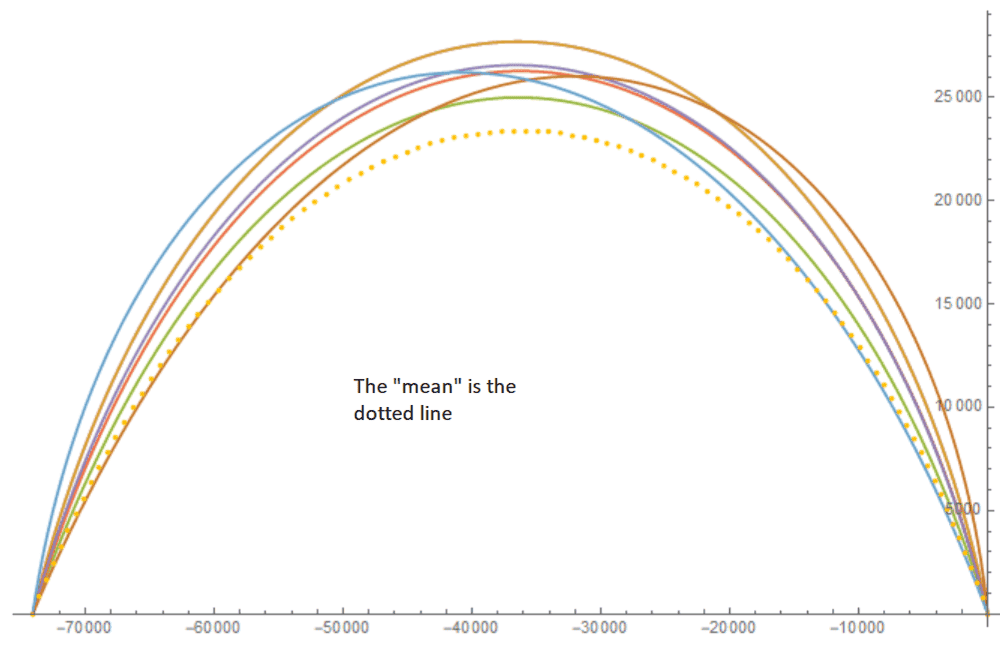
Then, if l+1=2 and l+d =4, I should add all the terms which are listed in the lexicographic matrix with |i|=2, 3 and 4. However, since the terms which have a zero as one of the index don't have nodes, these are discarted, leaving me with (1 1 1), (2 1 1) and (1 1 2), which in total produce 7 realizations. However, if I use these realizations, my mean looks signifficantly different from the realizations as can be seen in the figure.

For what I have read, the amount of realizations that should be used is way higher than 7; however, I cannot find where my mistake is.

Any answer is appreciaded.
Thanks.

 

[fresh_42]

I do not understand the setup, but for the tensor product we have $u\otimes v = \lambda u \otimes \frac{1}{\lambda} v$ and therefore many possible variations of the same tensor; plus possible symmetries of order.