Solve Arrow Head Geometry Question with L1, L2 & L3

[nucloxylon]

Homework Statement

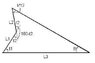
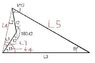
I have this arrow head geometry question (Please see diagram). I know L1, L2 and L3, angle B and the constant k (notice how the corner angle is equal to k * t2). I don't know t1 and t2. I'm pretty sure I have enough constraints, I'm just having trouble finding the right ones to use. Note that the arrow head is not symmetric so the top edge length is not equal to L3.

Homework Equations

Knowns:
L1
L2
L3
B
k

unknowns:
t1
t2

The Attempt at a Solution

The sum of the interior angles gives me one equation:
360 = t1 + t2+ 180 - t2 + t2 + k*t2 + B
B = 180 - t1 - t2 - kt2

Now I tried using the lengths and forming some equations using the cosine rule. I split the arrow head down the middle (gaining a length Lm), so I have
Lm^2 = L1^2 + L3^2 - 2*L1*L3*cos(t1)

but then I don't have the top edge as I mentioned, so I can't really equate this to anything.

I'm kind of stumped, any help would be appreciated!

 

[susskind_leon]

I would first pretend to know t1 and t2, write down some relations and see if it's possible to solve for t1, t2.
My approach would be to draw a new line L4 that closes the arrow on the left side.
Then you can compute it's length using the law of cosines and the angle t2 (or 180°-t2).
THEN, you've got enough parameters to compute the angle between L4 and L2, let's call it t3.
THEN, you could compute the length of the top line, let's call it L5, using again the law of cosines and the angle B.
THEN, you can compute the angle between L4 and L3, let's call it t4 and you finally have
t1=t4-t3, which "closes the circle". See if you like my approach and if so, try to do the calculations.