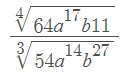Help Needed: Solving x and Simplifying Equations

  • Context: MHB 
  • Thread starter Thread starter bigpoppapump
  • Start date Start date
  • Tags Tags
    Simplifying
Click For Summary
SUMMARY

This discussion focuses on solving equations and simplifying expressions in trigonometry and electrical circuit analysis. Key techniques include substituting $\sin^2{x}$ with $(1-\cos^2{x})$ to solve quadratic equations for $\cos{x}$, and converting cosecant and cotangent into sine and cosine factors for simplification. A specific example involves modeling an electrical circuit's current as a function of time using the equation $A = 0.5 \sin\left(\dfrac{\pi}{10} \cdot t \right)$, accounting for a lag of 1 millisecond. Participants emphasize the importance of clearly stating where assistance is needed to facilitate effective help.

PREREQUISITES
  • Understanding of trigonometric identities and equations
  • Familiarity with quadratic equations
  • Basic knowledge of sinusoidal functions
  • Concept of alternating current (AC) and its frequency
NEXT STEPS
  • Learn how to apply trigonometric identities in solving equations
  • Explore the derivation and application of sinusoidal functions in AC circuit analysis
  • Study the effects of phase shifts in sinusoidal graphs
  • Investigate methods for converting word problems into mathematical equations
USEFUL FOR

Students and professionals in mathematics, electrical engineering, and physics who seek to enhance their problem-solving skills in trigonometry and circuit analysis.

bigpoppapump
Messages
5
Reaction score
0
having trouble with the following, if anyone could provide assistance it would be appreciated.

Solve for x:

1619175324265.png


and

Simplify the following:
1619175453718.png
 

Attachments

  • 1619175280121.png
    1619175280121.png
    1.2 KB · Views: 128
Mathematics news on Phys.org
Beer soaked request follows.
bigpoppapump said:
having trouble with the following, if anyone could provide assistance it would be appreciated.

Solve for x:

View attachment 11112

and

Simplify the following:
View attachment 11113
Please show us what you have tried and exactly where you are stuck.

We can't help you if we don't where you are stuck.
 
https://mathhelpboards.com/attachments/1619175324265-png.11112/
change $\sin^2{x}$ to $(1-\cos^2{x})$ and solve the resulting quadratic equation for $\cos{x}$https://mathhelpboards.com/attachments/1619175453718-png.11113/

change the cosecant and cotangent to factors in terms of sine & cosine, then simplify
 
skeeter said:
https://mathhelpboards.com/attachments/1619175324265-png.11112/
change $\sin^2{x}$ to $(1-\cos^2{x})$ and solve the resulting quadratic equation for $\cos{x}$https://mathhelpboards.com/attachments/1619175453718-png.11113/

change the cosecant and cotangent to factors in terms of sine & cosine, then simplify
Thank you. This helps, I was stuck but I have a good idea on how to solve both of these. Will work on it tonight.
 
I have managed to solved these problems with confidence which is great. Thanks for your guidance.

I have a word problem that I’m finding it difficult to convert into an equation. Could some direction be given so I can then run with it and complete.

The question is...
An electrical circuit runs at 50Hz at 0.5amps. Due to a lag in the switch, the first maximum current is reached at 6milliseconds. Assuming no variation, find an equation to model the current in this circuit using time in milliseconds.
 
frequency is the reciprocal of period (time to complete one cycle of AC)

$T = \dfrac{1}{50} = 0.02 \text{ sec } = 20 \text{ milliseconds}$

current flow (with no lag) as a function of time in milliseconds ...

$A = 0.5 \sin\left(\dfrac{\pi}{10} \cdot t \right)$

For that period, the sinusoidal graph of current would peak at $\dfrac{T}{4} = 5 \text{ milliseconds}$

Due to the lag, there is a 1 millisecond horizontal shift in the graph ...

In future, please start a new problem with a new thread.
 
Last edited by a moderator:

Similar threads

Undergrad Can x be found for ax^b - x^(b-2) = c in the general form?
  • · Replies 3 ·
Replies
3
Views
952
MHB Simplifying and expanding expressions
  • · Replies 5 ·
Replies
5
Views
2K
High School Can this equation be simplified?
  • · Replies 7 ·
Replies
7
Views
2K
Undergrad How to solve an equation with FMOD in it
  • · Replies 10 ·
Replies
10
Views
1K
MHB Need Help Solving x^2-x-4=0? Get Assistance Here!
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Trouble Solving an Equation that has square roots on both sides
  • · Replies 1 ·
Replies
1
Views
2K
High School What is the use of simplifying a question in math?
  • · Replies 3 ·
Replies
3
Views
1K
Graduate Find the Equation of a Line (not simple)
  • · Replies 12 ·
Replies
12
Views
2K
MHB Solve $x^4+(4-x)^4=32$ Equation
  • · Replies 2 ·
Replies
2
Views
1K
High School Missing out on intermediate algebraic steps
  • · Replies 23 ·
Replies
23
Views
2K