Solving a Differential Equation: dy/dt = t/(y + 1)

[magnifik]

Can someone help me find the solution for this

dy/dt = t/(y + 1) with initial condition y(2) = 0

here's what i have done so far
(y + 1) dy = t dt
y²/2 + y = t²/2 + C

i am confused on how to isolate y.
this is the solution

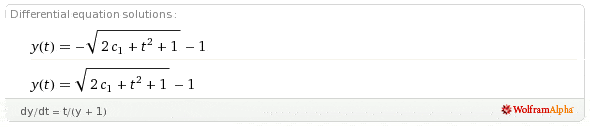without using the initial condition. where did the + 1 in the square root and - 1 outside of the square root come from?

 

[Char. Limit]

First, multiply both sides by 2. Then complete the square on the LHS.

 

[SammyS]

Don't forget, use y(2)=0, to evaluate C. (or c₁).

 

[TJ@UNF]

After you've separated your variables and integrated both sides (which you have done correctly), multiply both sides by 2 to get rid of your coefficents and take the square root of both sides to solve for t. Then apply your condition.

 

[HallsofIvy]

After you've separated your variables and integrated both sides (which you have done correctly), multiply both sides by 2 to get rid of your coefficents and take the square root of both sides to solve for t. Then apply your condition.

Once you have multiplied both sides by 2, you will still have y^2+ 2y on the left side and just "taking the square root" won't give you y. Complete the square as Char. Limit said in the very first response to this thread.

 

[magnifik]

Thanks for the help!