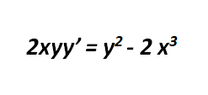SUMMARY
The discussion focuses on solving the first order linear differential equation given by \(xu' - u = -2x^3\) with the initial condition \(y(1) = 2\), which translates to \(u(1) = 4\) where \(u = y^2\). The substitution \(x = u + 1\) and \(y = v + 2\) was initially attempted but did not yield a solution. The correct approach involves reducing the equation to its linear form and applying the initial value problem (IVP) to find the specific solution that meets the initial condition.
PREREQUISITES
- Understanding of first order linear differential equations
- Familiarity with initial value problems (IVP)
- Knowledge of substitution methods in differential equations
- Basic calculus, particularly derivatives and integration
NEXT STEPS
- Study the method of integrating factors for solving linear differential equations
- Learn about the existence and uniqueness theorem for initial value problems
- Explore substitution techniques in differential equations
- Practice solving various forms of first order linear differential equations
USEFUL FOR
Students and professionals in mathematics, particularly those studying differential equations, as well as educators looking for examples of solving initial value problems.