I'm still confused about this one.

Seems to me that it all depends on how we define $y^{\frac 2 3}$.
Is it defined for negative y or not?
I'm used to treating it as defined, although most calculators cannot handle it.
Anyway, if $y^{\frac 2 3}$ is not defined for negative y, we cannot get solutions if $a < 0$, since the ODE is not defined then.
If $y^{\frac 2 3}$
is defined for negative y, I believe there is no special restriction.
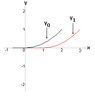
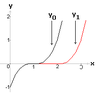
Any solution can be constructed from the 3 parts, with either the leftmost or the rightmost part fixed by a value of $a \ne 0$.
And, depending on $a$, the leftmost or rightmost part can also be zero.
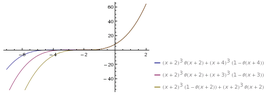
If we pick $y=x^3$ for $x < 0$, we get:
$$\begin{aligned}y'&=3x^2 &> 0\\
3y^{\frac 2 3} &= 3(x^3)^{\frac 2 3} = 3x^2 &> 0 \end{aligned}$$
So the ODE is satisfied.