Solving for AB & AC: Find the Solution

[paulmdrdo1]

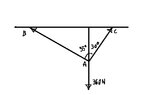
Find AB and AC in the figure given.

I came up with 2 equations which have 3 unknowns,

$AB\sin(55)+AC\sin(30)=BC$
$AB\sin(35)=AC\sin(60)$

I'm not sure if I'm just missing some given in the problem. Because if BC is given I can solve the equation above. Please help. thanks!

 

[MarkFL]

First, let's resolve the 3 forces into their $x$ and $y$ components (where point $D$ is directly below $A$, the mass):

Force	$x$-component	$y$-component
$\vec{AB}$	$-\vec{AB}\sin\left(55^{\circ}\right)$	$\vec{AB}\cos\left(55^{\circ}\right)$
$\vec{AC}$	$\vec{AC}\sin\left(30^{\circ}\right)$	$\vec{AC}\cos\left(30^{\circ}\right)$
$\vec{AD}$	$0$	$-360\text{ N}$

Now, the first condition for equilibrium gives us the equations:

\(\displaystyle \sum F_x=\vec{AC}\sin\left(30^{\circ}\right)-\vec{AB}\sin\left(55^{\circ}\right)=0\)

\(\displaystyle \sum F_y=\vec{AB}\cos\left(55^{\circ}\right)+\vec{AC}\cos\left(30^{\circ}\right)-360\text{ N}=0\)

Now, you have two equations in two unknowns. :D