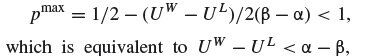SUMMARY
The discussion focuses on the mathematical inequality involving variables $\alpha$ and $\beta$, specifically addressing the expression $(U^W - U^L) < \alpha - \beta$. The key conclusion is that the inequality holds true only when $\alpha > \beta$. The participants clarify the steps to derive the inequality, emphasizing the importance of correctly ordering $\alpha$ and $\beta$ to avoid errors in the final expression. The discussion provides a clear method for manipulating the inequality through subtraction and multiplication, ensuring accurate results.
PREREQUISITES
- Understanding of basic algebraic manipulation
- Familiarity with inequalities in mathematical expressions
- Knowledge of variables and their relationships in equations
- Experience with mathematical notation, particularly involving inequalities
NEXT STEPS
- Study the properties of inequalities in algebra
- Learn about the implications of variable ordering in mathematical expressions
- Explore advanced topics in mathematical proofs involving inequalities
- Review examples of inequalities in economic theory, particularly in utility functions
USEFUL FOR
Students, mathematicians, and economists who are working with inequalities in mathematical models, particularly those involving utility functions and comparative statics.