Solving Linear Programming Problems Graphically

[evinda]

The following linear programming problem is given and I want to solve it graphically.

$$\max (x-y) \\ x+y \leq 4 \\ 2x-y \geq 2 \\ x,y \geq 0$$

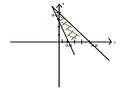
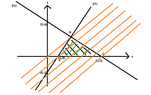
I have drawed the lines :

$$(\ell_1) x+y=4 \\ (\ell_2) 2x-y=2 \\ (\ell_3) x=0 \\ (\ell_4) y=0$$

as follows:

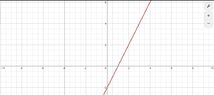
View attachment 5092I have drawed the line $2x-y=0$ taking into consideration the following:

For $y=0 \Rightarrow x=1$ and for $y=2 \Rightarrow x=\frac{1}{2}$.But I found that this is the graph of $2x-y=2$ :View attachment 5093

So are the points that I have found above wrong? Or where is my mistake? (Thinking)

 

[I like Serena]

Hey evinda! (Smile)

In your drawing you have the line $2x+y=2$ instead of the line $2x-y=2$.

 

[evinda]

Hey evinda! (Smile)

In your drawing you have the line $2x+y=2$ instead of the line $2x-y=2$.

If we take pick $y=0$ we get $x=1$ and if we pick $y=2$ we get $x=2$.

Then we would get a line like this:
View attachment 5094

But picking $y=-2 \Rightarrow x=0$ and $y=1 \Rightarrow x=\frac{3}{2}$ we get a line as below:

View attachment 5095

Or am I wrong? (Thinking)

 

[I like Serena]

Your first line is for $2x+y=2$ while the second is for $2x-y=2$.
It should be like the second.

Note that if we substitute $y=2$ in $2x-y=2$, we get $-2=2$.

 

[evinda]

Your first line is for $2x+y=2$ while the second is for $2x-y=2$.
It should be like the second.

Note that if we substitute $y=2$ in $2x-y=2$, we get $-2=2$.

Yes, I noticed it too now... I am sorry... Thank you! (Smile)

I will try to find now the optimal solution...

 

[evinda]

We also draw at the same graph the line $x-y=0$.
We consider the line $x-y=\lambda, \lambda>0$ where $\lambda$ is increasing.

View attachment 5096

Do we deduce from the graph that the optimal solution is $C(4,0)$ since it is the last line? (Thinking)

 

[I like Serena]

Do we deduce from the graph that the optimal solution is $C(4,0)$ since it is the last line? (Thinking)

Yep. (Nod)

 

[evinda]

Yep. (Nod)

Nice...And how could we explain it more formally? (Thinking)

 

[I like Serena]

Nice...And how could we explain it more formally? (Thinking)

Erm... I believe that for the graphical method this is pretty much it.
The formal method is with a simplex tableau. (Emo)

 

[evinda]

Erm... I believe that for the graphical method this is pretty much it.
The formal method is with a simplex tableau. (Emo)

A ok... Thanks a lot! (Smirk)