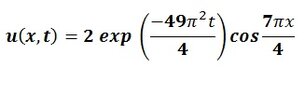Discussion Overview
The discussion revolves around solving the one-dimensional heat equation using the method of separation of variables. Participants explore the equation given by \(\frac{\partial u}{\partial t}=4\frac{\partial^2 u}{\partial x^2}\) with specific boundary and initial conditions. The focus is on deriving a solution for the temperature \(u(x,t)\) under these constraints.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant expresses difficulty in solving the heat equation and seeks assistance.
- Another participant proposes a solution using separation of variables, leading to a pair of ordinary differential equations (ODEs) for \(\alpha(x)\) and \(\beta(t)\).
- It is noted that the boundary conditions provided may not be coherent with the initial condition, particularly at \(x=0\).
- A later reply suggests that the initial condition can be redefined to allow for a Fourier series representation, leading to a different form of the solution.
- Confusion arises when a participant mentions their professor's claim of a different correct answer, which adds to the uncertainty regarding the solution.
- Another participant points out a potential typo in the initial problem statement regarding the boundary conditions, suggesting that the conditions should involve partial derivatives.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct interpretation of the boundary conditions or the resulting solution. There are competing views on the coherence of the initial conditions and the validity of the proposed solutions.
Contextual Notes
The discussion highlights limitations in the clarity of the problem statement, particularly regarding the boundary conditions. There are unresolved mathematical steps and assumptions about the nature of the initial condition that affect the proposed solutions.