Solving the Representation of d/dq: Mistake in Reasoning?

[Spin One]

When considering the position representation of a system with one degree of freedom endowed with canonical co-ordinates and momenta q and p, Dirac deduces that:

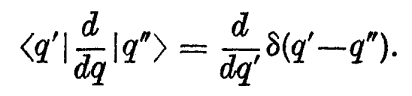
which is the representation of d/dq in "matrix" form. But the derivative of a delta function is, I assume (from the definition of the delta function), of the form

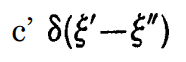, with ξ' and ξ" interchanged for q' and q", since the gradient of the delta function will be 0 everywhere except at q'=q", where it will be undefined.
So the representation of d/dq is a scalar "matrix" in the q representation(from the definition)
But the momentum operator is just iħd/dq, meaning it is a scalar matrix too.
q is of course also a scalar matrix (since the representation is built upon it), and since scalar matrices commute, we get that:
pq-qp=0, which contradicts the quantum condition pq-qp=iħ.

There must be a mistake in my line of reasoning, and I would much appreciate it if someone can point it out.

 

[Orodruin]

But the derivative of a delta function is, I assume (from the definition of the delta function), of the form

, with ξ' and ξ" interchanged for q' and q", since the gradient of the delta function will be 0 everywhere except at q'=q", where it will be undefined.

This is an incorrect assumption. The derivative of the delta distribution is different from the delta distribution itself. Instead of having the property
$$
\int f(x) \delta(x) dx = f(0)
$$
as the delta distribution, it has the property
$$
\int f(x) \delta'(x) dx = - \int f'(x) \delta(x) dx = -f'(0).
$$

 

[Spin One]

This is an incorrect assumption. The derivative of the delta distribution is different from the delta distribution itself. Instead of having the property
$$
\int f(x) \delta(x) dx = f(0)
$$
as the delta distribution, it has the property
$$
\int f(x) \delta'(x) dx = - \int f'(x) \delta(x) dx = -f'(0).
$$

Oh ok, thanks! I see now how my intuition was wrong, since taking the δ function in the sense of a limit of a proper function, the derivative must be 0 at δ(0), +∞ at δ(-ε) and -∞ at δ(+ε). In that case, will the representation of d/dq be a "matrix" (of the generalized kind) with only two diagonals just above and just below the main diagonal having a non-zero value?