Tangent space basis vectors under a coordinate change

[Shirish]

I'm studying 'Core Principles of Special and General Relativity' by Luscombe - the chapter on tensors.

Quoting:

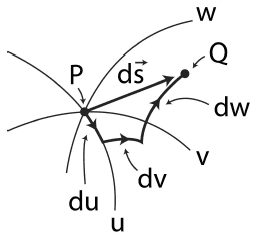
Consider an arbitrary three-dimensional coordinate system where point $P$ is at the intersection of three coordinate curves labeled by $(u,v,w)$. For a nearby point $Q$ define the vector $\Delta \mathbf{s}\equiv\vec{PQ}$; $\Delta \mathbf{s}$ is also the vector $\Delta \mathbf{s}=(\mathbf{r}+\Delta\mathbf{r})-\mathbf{r}$, where $\mathbf{r}+\Delta\mathbf{r}$ and $\mathbf{r}$ are the position vectors for $Q$ and $P$ relative to the origin. To first order in small quantities,$$d\mathbf{s}=\frac{\partial\mathbf{r}}{\partial u}du+\frac{\partial\mathbf{r}}{\partial v}dv+\frac{\partial\mathbf{r}}{\partial w}dw$$ where the derivatives (with respect to the coordinates) are evaluated at $P$. The derivatives $$\mathbf{e}_u\equiv \frac{\partial \mathbf{r}}{\partial u}, \mathbf{e}_v\equiv \frac{\partial \mathbf{r}}{\partial v}, \mathbf{e}_w\equiv \frac{\partial \mathbf{r}}{\partial w}$$ form a local basis - an arbitrary $d\mathbf{s}$ in the neighborhood of $P$ can be expressed as a linear combination of them - and they're tangent to the coordinate curves.

The book goes on to talk about a switch to the spherical coordinate system, in which $\mathbf{r}$ is specified as:
$$\mathbf{r}=r\sin\theta\cos\phi\ \mathbf{\hat x}+r\sin\theta\sin\phi\ \mathbf{\hat y}+r\cos\theta\ \mathbf{\hat z}$$And from this we get the expressions:
\begin{equation}
\begin{split}
\mathbf{e}_r&=\frac{\partial \mathbf{r}}{\partial r}&=\sin\theta\cos\phi\ \mathbf{\hat x} + \sin\theta\sin\phi\ \mathbf{\hat y} + \cos\theta\ \mathbf{\hat z} \\
\mathbf{e}_{\theta}&=\frac{\partial \mathbf{r}}{\partial \theta}&=r\cos\theta\cos\phi\ \mathbf{\hat x} + r\cos\theta\sin\phi\ \mathbf{\hat y} - r\sin\theta\ \mathbf{\hat z} \\
\mathbf{e}_{\phi}&=\frac{\partial \mathbf{r}}{\partial \phi}&=-r\sin\theta\sin\phi\ \mathbf{\hat x} + r\sin\theta\cos\phi\ \mathbf{\hat y}
\end{split}
\end{equation}Fair enough so far. I'm simultaneously reading 'A Visual Introduction to Differential Forms and Calculus on Manifolds' by Fortney. In that, a vector $v_p$ in the tangent space $T_p(\mathbb{R}^3)$ is defined as an operator acting on a real function $f$ defined on the manifold (i.e. $f:\mathbb{R}^3\to\mathbb{R}$). The operator gives the directional derivative of $f$ in the direction $v_p$ at point $p$:
$$v_p[f]=\sum_{i=1}^3v_i\frac{\partial f}{\partial x^i}\ \bigg|_p$$From this, we can identify the basis vectors of $T_p(\mathbb{R}^3)$ as:
$$\frac{\partial}{\partial x^1}\ \bigg|_p,\frac{\partial}{\partial x^2}\ \bigg|_p,\frac{\partial}{\partial x^3}\ \bigg|_p$$which, as you can see, are quite different from the basis vectors $\mathbf{e}_u,\mathbf{e}_v,\mathbf{e}_w$ that I defined at the start of the question.

So now let's say I switch to spherical coordinate system and want to specify the tangent space basis vectors in the spherical coordinate representation. And I want to reconcile those basis vectors' spherical representation with the $\mathbf{e}_r,\mathbf{e}_{\theta},\mathbf{e}_{\phi}$ formulas from the Luscombe book that I listed at the beginning.

Now you've seen that the Luscombe book formulas for $\mathbf{e}_r,\mathbf{e}_{\theta},\mathbf{e}_{\phi}$, that I listed at the start, contain $\mathbf{r}$. My interpretation of $\mathbf{r}$ is that it's a function from $\mathbb{R}^3\to\mathbb{R}$, and it's a triple consisting of the three coordinate functions required to specify coordinates of any point $p$ in the manifold $\mathbb{R}^3$. We can specify $\mathbf{r}=(x,y,z)$, where
\begin{equation}
\begin{split}
x&=x(r,\theta,\phi)&=r\sin\theta\cos\phi \\
y&=y(r,\theta,\phi)&=r\sin\theta\sin\phi \\
z&=z(r,\theta,\phi)&=r\cos\theta
\end{split}
\end{equation}are the individual coordinate functions. Since we've switched to spherical coordinates, we're now using the parameters $r,\theta,\phi$ to specify any point $p$ in the manifold $\mathbb{R}^3$.

Using the operator definition of tangent vectors, if I take $f=\mathbf{r}=(x,y,z)$ and $v_p=(\mathbf{e}_r)_p\implies v_r=1,v_{\theta}=0,v_{\phi}=0$, then
\begin{equation}
\begin{split}
(\mathbf{e}_r)_p[\mathbf{r}]&=v_r\frac{\partial \mathbf{r}}{\partial r}\ \bigg|_p+
v_{\theta}\frac{\partial \mathbf{r}}{\partial \theta}\ \bigg|_p+
v_{\phi}\frac{\partial \mathbf{r}}{\partial \phi}\ \bigg|_p=\frac{\partial \mathbf{r}}{\partial r}\ \bigg|_p \\
&=\frac{\partial}{\partial r}(r\sin\theta\cos\phi,r\sin\theta\sin\phi,r\cos\theta)\ \bigg|_p \\
&=(\sin\theta\cos\phi\,\sin\theta\sin\phi,\cos\theta)\ |_p
\end{split}
\end{equation} which matches the definition mentioned in the Luscombe book. Similarly we can calculate for the $\theta$ and $\phi$ basis vectors.

Two questions:
1. Does the above procedure of reconciling the two definitions for basis vectors seem correct?
2. If correct, to reconcile the definitions, I had to make a specific assumption about $f$ and act the math book version of the basis vector (as an operator) on $f=\mathbf{r}$ in order to actually get the physics book version of the same basis vector. Does that mean the physics book versions (formulas) of basis vectors are restrictive and will be incorrect in some scenarios? Or can I just take the physics book versions as the standard definition without worrying too much?

If you've read this far, thanks so much for the time and I'd appreciate any help!

 

[andrewkirk]

Yes, the physics book definition is restrictive, in fact very much so.

The physics book is treating the tangent space and the manifold to which it is tangent as the same thing. To see that, note that it uses vector $\mathbf r$ to refer to a point in the manifold. In general manifolds are not vector spaces, so it makes no sense to try to use a vector to refer to a point in the manifold. In particular, curved spaces like our spacetime are not vector spaces. So that conflation of the manifold with its tangent spaces can only work when the manifold is not curved and can be represented as a vector space.

If you want to study general relativity, the mathematical book's definition will serve you better, because it works for curved manifolds whereas the physics book's definition does not. Trying to use concepts where points in space are identified by vectors, as the physics book appears to do, is likely to lead to confusion.

 

[Shirish]

Yes, the physics book definition is restrictive, in fact very much so.

The physics book is treating the tangent space and the manifold to which it is tangent as the same thing. To see that, note that it uses vector $\mathbf r$ to refer to a point in the manifold. In general manifolds are not vector spaces, so it makes no sense to try to use a vector to refer to a point in the manifold. In particular, curved spaces like our spacetime are not vector spaces. So that conflation of the manifold with its tangent spaces can only work when the manifold is not curved and can be represented as a vector space.

If you want to study general relativity, the mathematical book's definition will serve you better, because it works for curved manifolds whereas the physics book's definition does not. Trying to use concepts where points in space are identified by vectors, as the physics book appears to do, is likely to lead to confusion.

Oh okay! So let's say I have some general manifold $M$ (in the context of general relativity). To find a local basis at some point $p\in M$, should I follow the procedure I detailed in the last part of my answer?

That is, given coordinate curves $p=p(x,y,z),q=q(x,y,z),r=r(x,y,z)$ (where $x,y,z$ are Cartesian), I can invert to get coordinate functions $x=x(p,q,r), y=y(p,q,r), z=z(p,q,r)$. Then I can apply the operators $\mathbf{e}_p,\mathbf{e}_q,\mathbf{e}_r$ to the function $\mathbf{r}=(x,y,z)$ to get the local basis vectors.

Does that sound right / is that how it's done?

 

[wrobel]

where are Cartesian

it is meaningless to say "Cartesian coordinates" in regard to a general manifold. Study the definition of a manifold

 

[Shirish]

it is meaningless to say "Cartesian coordinates" in regard to a general manifold. Study the definition of a manifold

You're right, I realized that and meant to edit my previous post, but can't do that. Edit: By $x,y,z$ I don't mean Cartesian, but some parametrization of the manifold $M$. If we change to some other parametrization $(p,q,r)$, would the procedure in the 2nd paragraph of my previous post hold?

 

[wrobel]

Then I can apply the operators to the function

it is not a function

 

[Shirish]

this is not a function

Another edit: ...then I can apply the operators... to $x,y,z$...

$\mathbf{r}$ is most definitely a function but not one to which we can directly apply the operators. Thanks for pointing it out!

 

[wrobel]

is most definitely a function

ok you know it better than me ,good luck

 

[Shirish]

ok you know it better than me ,good luck

I'm not claiming that I know better.

In my original post, I mentioned $\mathbf{r}$ as a $\mathbb{R}^3\to\mathbb{R}$ function, which is incorrect. But even so, wouldn't defining $\mathbf{r}$ as the triple $(x,y,z)$ make it a function from $\mathbb{R}^3\to\mathbb{R}^3$?

If you meant to say that $\mathbf{r}$ isn't a real-valued function, then you'd be right, but that wasn't mentioned in your post. Even if not a real-valued one, it's still a function regardless.

 

[Shirish]

Yes, the physics book definition is restrictive, in fact very much so.

The physics book is treating the tangent space and the manifold to which it is tangent as the same thing. To see that, note that it uses vector $\mathbf r$ to refer to a point in the manifold. In general manifolds are not vector spaces, so it makes no sense to try to use a vector to refer to a point in the manifold. In particular, curved spaces like our spacetime are not vector spaces. So that conflation of the manifold with its tangent spaces can only work when the manifold is not curved and can be represented as a vector space.

If you want to study general relativity, the mathematical book's definition will serve you better, because it works for curved manifolds whereas the physics book's definition does not. Trying to use concepts where points in space are identified by vectors, as the physics book appears to do, is likely to lead to confusion.

Another thing I wanted to clarify - my understanding is that if the spacetime geometry is flat, then intuitively speaking the tangent spaces are indistinguishable from the overall manifold, and so we can get away with assigning a vector space structure to the manifold itself, and we can get away with not talking about tangent spaces in that case. Does that sound correct?

Also, I realize there's a rigorous definition of the curvature of a manifold, but intuitively speaking how do we tell if a manifold (i.e. the spacetime geometry) is flat or curved? I mean, the contours/coordinate curves of the manifold must be curved with respect to something or some reference curve, right? So do we consider the manifold to be embedded within some ambient flat 4D space? [You can ignore this question if it's not possible to answer it intuitively btw. Apologies if it doesn't make much sense]

 

[andrewkirk]

I realize there's a rigorous definition of the curvature of a manifold, but intuitively speaking how do we tell if a manifold (i.e. the spacetime geometry) is flat or curved? I mean, the contours/coordinate curves of the manifold must be curved with respect to something or some reference curve, right? So do we consider the manifold to be embedded within some ambient flat 4D space? [You can ignore this question if it's not possible to answer it intuitively btw. Apologies if it doesn't make much sense]

A manifold is flat if its Riemann curvature tensor is everywhere zero. That is a coordinate-independent property, meaning it is not affected by the choice of coordinate system. It is also not affected by any embedding in another space.

Geometry recognises two types of curvature: intrinsic curvature, which is measured by the curvature tensor and extrinsic curvature. Extrinsic curvature is only meaningful when the manifold is embedded in another manifold - typically a higher-dimensional space. It relates to how the embedding is done.

The classic example of extrinsic curvature is making a cylinder by pasting together opposite sides of a square. The cylinder is a 2D manifold that has extrinsic curvature, because it 'curves' through the 3D space in which it is embedded. But it has no intrinsic curvature because its curvature tensor will be everywhere zero. In contrast, the surface of a sphere has intrinsic curvature, regardless of whether it is embedded in our usual 3D space or in some other higher-dimensional space. In loose terms, that's because you can flatten a cylinder without tearing or stretching it, but you can't do that to a sphere.

 

[Shirish]

Yes, the physics book definition is restrictive, in fact very much so.

The physics book is treating the tangent space and the manifold to which it is tangent as the same thing. To see that, note that it uses vector $\mathbf r$ to refer to a point in the manifold. In general manifolds are not vector spaces, so it makes no sense to try to use a vector to refer to a point in the manifold. In particular, curved spaces like our spacetime are not vector spaces. So that conflation of the manifold with its tangent spaces can only work when the manifold is not curved and can be represented as a vector space.

Thanks a lot for your help so far!

So I was referring to another book 'A Most Incomprehensible Thing - Notes towards a very gentle introduction to the mathematics of relativity'. It talks about tangent space basis vectors as the usual derivative operators and the cotangent space dual basis vectors as differentials. But then it later goes on to say, after a discussion on curved spacetime, so we know that he's not talking exclusively in the context of flat spacetime:

Both contravariant vectors and basis one-forms are also defined in terms of derivatives of the coordinate functions.

Again, doesn't this become restrictive in any way, or is this definition equivalent to the usual definition of basis vectors as derivative operators and basis covectors as differentials?

The way I'm interpreting it is, if we consider basis vectors in terms of derivatives of coordinate functions, then we're selecting a particular basis, i.e. the one whose elements are tangent to the coordinate curves passing through that point.
Similarly considering dual basis vectors as differentials of coordinate functions means we're selecting a particular dual basis whose elements measure the change in the coordinate curve "level sets" as we move along a vector.

The general definitions of the bases allow us to select arbitrary choice of basis and dual basis. Does that sound correct?

 

[andrewkirk]

"Both contravariant vectors and basis one-forms are also defined in terms of derivatives of the coordinate functions."
It would be more accurate to say 'can also be defined in terms of ...'. We don't need a coordinate system to define those things, but we often use one because it's convenient.

The way I'm interpreting it is, if we consider basis vectors in terms of derivatives of coordinate functions, then we're selecting a particular basis, i.e. the one whose elements are tangent to the coordinate curves passing through that point.

Yes that's right. We are selecting the 'coordinate basis' of that coordinate system. A non-coordinate basis is a basis that is not the coordinate basis of any coordinate system.

Similarly, a 'coordinate dual basis' can be derived from a coordinate system based on level sets.

Just a minor technical point. A basis is an independent set of vectors that spans the tangent space at a single point on the manifold. When we are talking about the bases for tangent spaces of all the points in a patch of the manifold, we are actually talking about a 'basis field' or a 'frame field', which is a collection of n vector fields on that patch (n being the dimension of the manifold), each of which maps each point to a basis vector in the tangent space at that point. But for shorthand we often just use 'basis' to refer to the basis field.

The general definitions of the bases allow us to select arbitrary choice of basis and dual basis.

I wouldn't say arbitrary. Firstly, there are conditions a set of vectors needs to satisfy to qualify as a basis. Secondly, the dual basis is fully determined once we have selected the basis. But we can choose any valid local coordinate system and use the basis and dual basis that are derived from that.