Solving the Wallis Product: Constructing Rectangles for $\pi/2$

[DivGradCurl]

Folks, I have a problem in my calculus textbook about the Wallis Product

\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \cdots

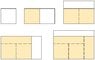
"We construct rectangles as follows. Start with a square of area 1 and attach rectangles of area 1 alternately beside or on top of the previous rectangle (see figure). Find the limit of the ratios of width to height of these rectangles."

Here's what I've got:

R_1 = \frac{W_1}{H_1} = \frac{1}{1} = 1

R_2 = \frac{W_2}{H_2} = \frac{W_1 + \frac{1}{H_2}}{H_1} = \frac{2}{1} = 2

R_3 = \frac{W_3}{H_3} = \frac{W_2}{H_2 + \frac{1}{W_3}} = \frac{2}{3/2} = \frac{4}{3}

R_4 = \frac{W_4}{H_4} = \frac{W_3 + \frac{1}{H_4}}{H_3} = \frac{8/3}{3/2} = \frac{16}{9}

R_5 = \frac{W_5}{H_5} = \frac{W_4}{H_4 + \frac{1}{W_5}} = \frac{8/3}{15/8} = \frac{64}{45}

Since all previous parts of this problem are about the Wallis Product, it would not be surprising to find out that the limit of the ratios of width to height of those rectangles is \frac{\pi}{2}. It doesn't seem to be appropriate to simply state it, though.

If n is even, then

W_n = W_{n-1} + \frac{1}{H_n} and H_n = H_{n-1}

and so

R_n = \frac{W_n}{H_n} = \frac{W_{n-1} + \frac{1}{H_n}}{H_{n-1}}

If n is odd, then

W_n = W_{n-1} and H_n = H_{n-1} + \frac{1}{W_n}

and so

R_n = \frac{W_n}{H_n} = \frac{W_{n-1}}{H_{n-1} + \frac{1}{W_n}}

Thus, we find


\lim _{n\to \infty} \frac{W_{n-1} + \frac{1}{H_n}}{H_{n-1}} = \lim _{n\to \infty} \frac{W_{n-1}}{H_{n-1} + \frac{1}{W_n}}

However, I don't know how to proceed so that I find

\lim _{n\to \infty} R_n = \frac{\pi}{2}

Any help is highly appreciated. Thanks.

PS: THE FIGURE IS ATTACHED.

 

[OlderDan]

First, I think you want to express each ratio in terms of heights and widths of previous terms, not in terms of the current term. Then be sure to keep the H and W identifiable before reducing the fractions and leave the fractions factored. I added an intermediate step that you have done correctly, and idenitfied the W and H for each term in brackets.

R_1 = \frac{W_1}{H_1} = \frac{1}{1} = 1

R_2 = \frac{W_2}{H_2} = \frac{W_1 + \frac{1}{H_1}}{H_1} = \frac{1 + 1}{1}= \left[\frac{2}{1}\right] = 1\cdot\frac{2}{1}

R_3 = \frac{W_3}{H_3} = \frac{W_2}{H_2 + \frac{1}{W_2}} = \frac{2}{1 + 1/2} = \left[\frac{2}{3/2}\right] = 1\cdot\frac{2}{1}\cdot\frac{2}{3}

R_4 = \frac{W_4}{H_4} = \frac{W_3 + \frac{1}{H_3}}{H_3} = \frac{2 + 2/3}{3/2} = \left[\frac{8/3}{3/2}\right] = 1\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}

R_5 = \frac{W_5}{H_5} = \frac{W_4}{H_4 + \frac{1}{W_4}} = \frac{8/3}{3/2+3/8}= \left[\frac{8/3}{15/8}\right] = 1\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot\frac{4}{5}

R_6 = \frac{W_6}{H_6} = \frac{W_5 + \frac{1}{H_5}}{H_5} = \frac{8/3+8/15}{15/8} = \left[\frac{16/5}{15/8}\right] = 1\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot\frac{4}{5}\cdot\frac{6}{5}

R_7 = \frac{W_7}{H_7} = \frac{W_6}{H_6 + \frac{1}{W_6}}= \frac{16/5}{15/8+5/16} = \left[\frac{16/5}{35/16}\right] = 1\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot\frac{4}{5}\cdot\frac{6}{5}\cdot\frac{6}{7}

By keeping the fractional factors, you see the progression as the Wallis Product, so if you believe the given expansion, you have shown the ratio of the rectangle sides has the \pi/2 limit.

 

[DivGradCurl]

That's definitely it! Thank you very much.