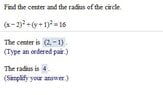SUMMARY
The discussion focuses on the equation of a circle in the Cartesian plane, represented as $$(x-h)^2+(y-k)^2=r^2$$. The center of the circle is denoted by the coordinates $(h,k)$, while $r$ represents the radius. An example is provided with the circle centered at $(2,-1)$ and a radius of $4$. The conversation also clarifies that the parameters $h$ and $k$ are arbitrary and can be replaced with other symbols such as $(a,b)$ without affecting the mathematical principles involved.
PREREQUISITES
- Understanding of Cartesian coordinates
- Familiarity with the equation of a circle
- Basic knowledge of the Pythagorean theorem
- Ability to manipulate algebraic expressions
NEXT STEPS
- Study the derivation of the circle equation from the distance formula
- Explore transformations of geometric figures in the Cartesian plane
- Learn about different coordinate systems and their applications
- Investigate the use of parameters in mathematical equations
USEFUL FOR
Students studying geometry, educators teaching mathematics, and anyone interested in understanding the properties of circles and their equations.