Speed of a satellite above the earth?

[Tangeton]

(b) (i) A satellite of mass 2520 kg is at a height of 1.39 × 10⁷m above the surface of the Earth. Calculate the gravitational force of the Earth attracting the satellite. Give your answer to an appropriate number of significant figures.
Worked out to be F = 2.45 x 10³
The satellite in part (b)(i) is in a circular polar orbit. Show that the satellite would travel around the Earth three times every 24 hours.

The answer is F = (mv²)/R+h where F = 2.45 x10³ to find the speed first.

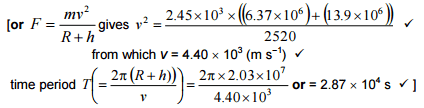
But no matter how I put that equation into the calculator, whether I use the valued stored in the calculator or type in exactly what it says, it is not 4.40 for speed but 4.439... so 4.44. Why is that?

This is a past exam question.

 

[BvU]

√The answer is not F = (mv²)/R+h but F = mv²/(R+h) (if you don't want to type more than two brackets, use your energy effectively )
Never mind.

If I work out I $GMm\over (R+h)^2$, I get F = 2.44 10³ N, not 2.45 10³ N.
(m 2520 kg, h 13900000 m, R 6371000 m, R+h 20271000 m, G 6.67384E-11 m³ kg^-1 s^-2, M_earth 5.972E+24 kg $\Rightarrow$ GMm/(R+h)^2 = 2444.251 N, round off to 3 digits).
Never mind that, too. (Do correct me if I am wrong!)​

Then the book answer continues with that rounded off intermediate result and multiplies back with (R+h)/m to calculate yet another intermediary result, v. Again rounded off !

That is bad practice !​

It then continues to calculate a third intermediary result, T, and again rounds off. The final answer is not "T = 2.87 10⁴ s √ , but "3.00 orbits/day √".

One should calculate normally with the proper expression (in symbols) and round off only at the very end.​

The proper expression here starts with $$ {GMm\over(R+h)^2} = {mv^2\over (R+h)}\ \Rightarrow\ v^2 = {GM\over (R+h)} \ \Rightarrow\ v = \sqrt{GM\over(R+h)} $$

yielding v = 4434.148 m, but that's an intermediate result we don't even have to look at.
But I heartily agree with you they should not have typed 4.40 10³ !​

The proper expression continues (as shown) to$$ T = {2\pi (R+h) \over v} = 2\pi \sqrt{(R+h)^3\over GM}$$ and that can be properly rounded off if necessary (which it isn't really: 24*60*60/T = 3.0079382 is the thing that should be rounded off to 3.00).

So pfui to the book answer and bravo for you to not swallow that !

(since this is an exam question: in a real exam no one in his right mind would even think of deducting marks for a better-than-the-marking-scheme answer, so you have nothing to worry about.
And during the exam you don't have the answer, so you don't have to waste time on such a thing )

 

[Tangeton]

The proper expression here starts with $$ {GMm\over(R+h)^2} = {mv^2\over (R+h)}\ \Rightarrow\ v^2 = {GM\over (R+h)} \ \Rightarrow\ v = \sqrt{GM\over(R+h)} $$

yielding v = 4434.148 m, but that's an intermediate result we don't even have to look at.
But I heartily agree with you they should not have typed 4.40 10³ !​

The proper expression continues (as shown) to$$ T = {2\pi (R+h) \over v} = 2\pi \sqrt{(R+h)^3\over GM}$$ and that can be properly rounded off if necessary (which it isn't really: 24*60*60/T = 3.0079382 is the thing that should be rounded off to 3.00).

So pfui to the book answer and bravo for you to not swallow that !

(since this is an exam question: in a real exam no one in his right mind would even think of deducting marks for a better-than-the-marking-scheme answer, so you have nothing to worry about.
And during the exam you don't have the answer, so you don't have to waste time on such a thing )

Thank you for your answer. I get really worried when I see things like this in the marking scheme since it is hard to trust yourself over an exam paper.

Thank you also for taking your time to do the question as one expression it was interesting to observe what it becomes since I ended up getting frustrated with my answer for v and just decided to stick with working out ω and then T using T = 2π/ω.