Speed of Perigee: Find Satellite Velocity at 750 km

[cbarker1]

Dear Everybody,

How to get started for this problem?
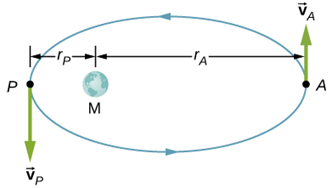
An Earth satellite has its apogee at 2,400 km above the surface of Earth and perigee at 750 km above the surface of Earth. At apogee its speed is 6,800 m/s. What is its speed at perigee (in m/s)? Earth's radius is 6,370 km (see the figure below, which is not drawn to scale)

Thanks,
Cbarker1

 

[I like Serena]

Can we apply conservation of energy?
$$E=E_p + E_k = -\frac{GMm}{r} + \frac 12 mv^2$$

 

[cbarker1]

yes. We can use the conservation of energy.

 

[I like Serena]

yes. We can use the conservation of energy.

Good.
So what's stopping you from getting the answer?

 

[I like Serena]

We need to find the potential energy and the kinetic energy at both the perigee and the apogee.
That should give us an equation from which we can find the answer. (Thinking)

 

[cbarker1]

We need to find the potential energy and the kinetic energy at both the perigee and the apogee.
That should give us an equation from which we can find the answer. (Thinking)

Do we need to find "M"?

 

[I like Serena]

Do we need to find "M"?

I think we need to look it up.
More specifically $\mu=GM=3.986004418(9)\times 10^{14}\text{ m}^3\text{s}^{-2}$. See wiki.

 

[skeeter]

conservation of momentum ...

$mv_Ar_A = mv_Pr_p$