- #1
mech-eng
- 828
- 13
How can I simulate this spring system and see how they move and behave?
Thank you.
Thank you.
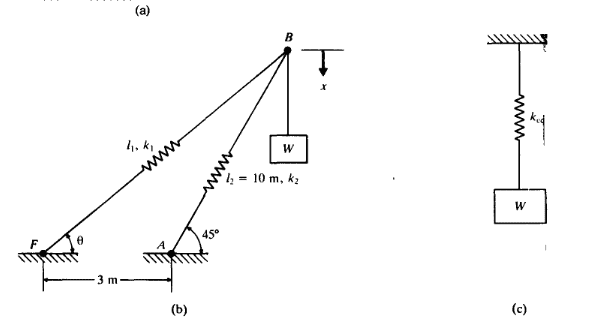
Looks like it's for schoolwork...mech-eng said:How can I simulate this spring system and see how they move and behave?
View attachment 206790
Thank you.
berkeman said:Looks like it's for schoolwork...
What simulation software do you have access to? Heck, you could even just simulate it in Excel and generate plots in Excel...
berkeman said:So it is for schoolwork, but sometimes simulation threads are allowed in the technical forums. We'll see how this goes, but you need to show LOTS of effort when posting advanced schoolwork in a technical forum..
I want to simulate that mass-spring system, a crane. No I would like to simuate springs with angles. I cannot imagine and understand how they will move, I cannot understand how their motion is.berkeman said:What are you simulating? Are you supposed to simulate the extensions of the springs based on different attached masses? Are you supposed to calculate some oscillations?
berkeman said:Try starting with Excel and just write the equations for the extensions of the springs as a function of the weights.
Well, the right-hand one (c) is easy, right? You write F=kx, displace the weight slightly from the equilibrium position, and write the equation of motion for the weight. Then in Excel you set up two columns, with the first column being time steps (say 1/100 of a second, or 1/10 of a second) starting at 0, and in the 2nd column you paste in the equation for the motion as a function of time. Then you can plot a graph of the motion of the weight as it oscillates vertically.mech-eng said:I do not know how I can write those equations. I know just F=kx for springs.
Yes, it is the easy one. Left side example is harder one to which I am more interested in.JBA said:An undamped spring and weight combination (the right side example) will always oscillate at it s natural frequency. Look up the equation for that category of vibration and you will get the appropriate equation for your time function simulation calculation.
Spring Simulation is a computer program that allows users to create and analyze moving systems, specifically those involving springs. Its purpose is to provide a visual representation of the movement and forces involved in these systems, allowing for a better understanding and analysis of their behavior.
The main features of Spring Simulation include the ability to create and manipulate objects, set different parameters such as mass and spring constants, apply forces and see their effect, and view the system in real-time or in slow motion.
Spring Simulation is primarily designed for systems involving springs, such as mass-spring systems, pendulums, and simple harmonic oscillators. However, it can also be used to simulate more complex systems that involve other types of forces and interactions.
The accuracy of the simulations in Spring Simulation depends on the input parameters and the complexity of the system being simulated. In general, the simulations provide a good representation of the behavior of the system, but they may not be fully accurate in all cases.
Yes, Spring Simulation can be a valuable educational tool for students learning about motion and forces. It allows for a hands-on approach to understanding these concepts and provides a visual representation that can aid in comprehension.