SUMMARY
The expression in question, 4 ln(x/(4+sqrt(16-x^2))), equals the reciprocal of its logarithm due to the properties of logarithms and absolute values. Specifically, for x in the intervals [-4,0) and (0,4], the expressions |(4+sqrt(16-x^2))/x| and |(4-sqrt(16-x^2))/x| multiply to 1, confirming they are reciprocals. Consequently, their logarithms are additive inverses, leading to the conclusion that the logarithm of one expression equals the negative of the logarithm of the other.
PREREQUISITES
- Understanding of logarithmic properties
- Familiarity with absolute values in mathematical expressions
- Basic knowledge of calculus concepts
- Ability to manipulate algebraic expressions
NEXT STEPS
- Study the properties of logarithms in depth
- Explore absolute value functions and their implications in calculus
- Learn about the behavior of functions defined by square roots
- Investigate the concept of multiplicative inverses in algebra
USEFUL FOR
Students of calculus, mathematics educators, and anyone interested in the properties of logarithmic functions and their applications in algebraic expressions.
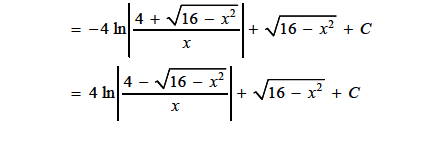 How come the above expression equals the below?
How come the above expression equals the below?