What Causes the High Tide on the Antipodal Side of the Earth?

[KurtLudwig]

Please explain high tide at antipodal side as described in Wikipedia https://en.wikipedia.org/wiki/Tide diagram.
At the sublunar side of the earth, sea water is attracted by the moon causing a high tide. On the antipodal side of the Earth sea water is also attracted, somewhat less since the antipodal side is further away from the moon. There should be a trough at the antipodal side, but it is shown as a high tide. There is also a daily high tide due to the sun, but at a lower amplitude. If there were two high tides due to the moon and two lower high tides due to the sun, then there would be four high tides per day, which is not correct.

 

[.Scott]

Let's say that we had a completely liquid planet with a large moon.
The average pull on the planet would cause the planet to move. So if we are interested in how the planet is shaped, we are interested in differences from this average. On the side facing the moon, there will be attraction towards the moon - the "up direction". Hence a high tide.
On the side facing away from the moon, there will be less attraction towards the moon. So it will move away from the moon relative to the average. That is also the up direction. Thus the liquid planet becomes elongated toward and away from the moon.

 

[anorlunda]

I like pictures. This illustrates what @.Scott said. A solid planet (yellow) near a liquid planet (blue).

 

[KurtLudwig]

Then each day, there will be two high tides due to the moon and, in addition, there will be two lower high tides due to the sun at a different phase. But we only observe about two high tides and two low tides each 24 hours.
On the side facing away from the moon, the sea water will be still attracted to the moon but to a lesser extent. Gravity only attracts. This will result in a lower sea level. I think Wikipedia is incorrect in this very rare instance.
Are you stating that the whole Earth deforms, with the sea bottom on the far side moving away from the moon? I tend to think that the sea water moves a little up, but is constrained by gravity, and moves mainly horizontally. I tend to think that the solid Earth does not deform much.

 

[anorlunda]

The tide due to the sun is hard to detect by itself. However, we do have "spring tides" (biggest variation) when the moon and the sun pull in the same or opposite directions, and "neap tides" (least variation) when they pull at 90 degree directions. So spring-neap-spring-neap in a lunar month.

But real life tides are more complicated. If you travel by boat around Florida, you will find two strong tides in the NE near Jacksonville, two unequal tides in southern Florida and the Keys, and only one noticeable tide as you move toward Panama City. The differences are caused by the profiles of the depth of the oceans within hundreds of miles of the shore. Sub-sea geometry complicates the picture.

 

[Bandersnatch]

Then each day, there will be two high tides due to the moon and, in addition, there will be two lower high tides due to the sun at a different phase. But we only observe about two high tides and two low tides each 24 hours.

That's not how you add up amplitudes. The wiki article explains this comprehensively, with animations and graphs. I'm not sure what more you'd like us to tell you to make it understandable other than to point to places in the article.
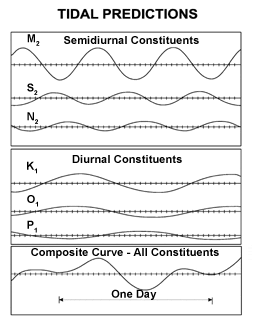
This is how various components add up:

As you can see in this example, despite six components in total, of different phases, amplitudes, and periods, the end result is still two high and two low.
This animation shows how the two principal components (solar and lunar) add up visually:

On the side facing away from the moon, the sea water will be still attracted to the moon but to a lesser extent. Gravity only attracts. This will result in a lower sea level. I think Wikipedia is incorrect in this very rare instance.

The wiki is not wrong - you just have a common misconception.

Look at this picture:

You start by noticing that the lines of gravitational force from a nearby massive body are not parallel (1)
As long as you treat the body as completely rigid, you only ever have to worry about the force on the centre of mass, expressed by Newton's law (2).
But since planets are not completely rigid, different parts of them will be deformed by relative differences in the strength and direction of the gravitational force (3). Parts closer to the massive body will be attracted more (F5) than the force on the centre of mass (F), parts farther will be attracted less (F4). Parts offset from the line connecting the centres of masses will be attracted in different directions (F2 & F3).

You can deduct the magnitude of the force vector acting on the centre of mass (F) from all other forces to find out the relative force w/r to the centre of mass of the planet. Since F>F4, the force resulting from deduction: F'=F4-F will be negative, i.e. it will be pulling away from the centre of mass. If you deduct F from F2 & F3, you'll end up with a component directed towards the CoM (roughly speaking).
If this weren't a semi-rigid planet, but a collection of loose particles, from the point of reference of the CoM, points 5 and 4 would be moving away due to the differences in the magnitude of acceleration, while points 2 and 3 would be moving closer due to the differences in direction.

If you repeat that process for all points on the surface, you end up with this picture (from wiki again):

Are you stating that the whole Earth deforms, with the sea bottom on the far side moving away from the moon? I tend to think that the sea water moves a little up, but is constrained by gravity, and moves mainly horizontally. I tend to think that the solid Earth does not deform much.

Since there is no such thing as a perfect rigid body, everything deforms. Parts that are more rigid deform less, parts that are more fluid deform more.
The crust deforms by centimetres, the oceans by metres, the atmosphere by kilometres.

 

[KurtLudwig]

I stand corrected.
Bandersnatch thanks so much for the detailed explanation. I fully understand now how to add wave shapes to get the result of only two high and two low tides of varying amplitudes.
Your vector analysis was most interesting. I do understand now how the vector sum F' became negative at the far side of the earth.
In he future, I will try to read Wiki articles more carefully.
Thanks again

 

[Metnic87]

Is the antipodal tide not mainly due to the resulting centrifugal force being strong enough at the farthest point of the Earth's surface from the moon, to pull water enough for it to be above the mean water level ? Resulting centrifugal force = centrifugal force due to Earth's rotation - opposite gravitational force.