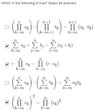Summation and product notation rules

Click For Summary
SUMMARY

The discussion focuses on the rules of summation and product notation, specifically addressing the validity of certain mathematical statements. The participant, Dan, identifies an incorrect statement regarding the distribution of a constant \( c \) across a product of terms. He asserts that \( c * (a_m*a_{m+1}*a_{m+2}*...*a_n) \) is not equivalent to \( (c*a_m)(c*a_{m+1})(c*a_{m+2})*...*(c*a_n) \). The consensus confirms that only two statements are valid, validating Dan's conclusion.

PREREQUISITES
  • Understanding of mathematical notation for summation and product.
  • Familiarity with properties of multiplication and distribution.
  • Basic knowledge of algebraic expressions and constants.
  • Ability to analyze and evaluate mathematical statements for correctness.
NEXT STEPS
  • Study the properties of summation and product notation in detail.
  • Learn about the implications of distributing constants in algebraic expressions.
  • Explore examples of valid and invalid statements in mathematical notation.
  • Review advanced topics in algebra that involve summation and product rules.
USEFUL FOR

Students, educators, and mathematicians interested in mastering summation and product notation rules, as well as anyone looking to clarify common misconceptions in algebraic expressions.

lemonthree
Messages
47
Reaction score
0
As per the image, I am supposed to select all the valid statements. Apparently I'm only partially correct, and so I took another look at the statements.

I believe the third statement is wrong, since $$c * (a_m*a_{m+1}*a_{m+2}*...*a_n)$$ =/= $$ (c*a_m)(c*a_{m+1})(c*a_{m+2})*...*(c*a_n)$$

Thus there should only be two answers. Am I correct on this?
 

Attachments

  • Capture.JPG
    Capture.JPG
    23.1 KB · Views: 141
Physics news on Phys.org
You are correct.

-Dan
 

Similar threads

Undergrad A Sequence T based on the Rule of Three
  • · Replies 15 ·
Replies
15
Views
2K
MHB Probability to get a chocolate snowman or a chocolate reindeer
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad ##(a_n) ## has +10,-10 as partial limits. Then 0 is also a partial limit
  • · Replies 13 ·
Replies
13
Views
2K
Undergrad Missing(?) rigor in proof involving countable union of countable sets
  • · Replies 10 ·
Replies
10
Views
2K
MHB Upper Bound of Sets and Sequences: Analyzing Logic
  • · Replies 3 ·
Replies
3
Views
5K
High School Continuation of sequence of supremums question
  • · Replies 9 ·
Replies
9
Views
1K
Undergrad ##(A/\mathfrak{a})_{\mathfrak{p}/\mathfrak{a}}## and its isomorphism?
  • · Replies 31 ·
2
Replies
31
Views
2K
Showing that a state is unentangled under a certain condition
  • · Replies 10 ·
Replies
10
Views
2K
MHB Indexed Families of Sets .... Just and Weese .... Exercise 8 ....
  • · Replies 1 ·
Replies
1
Views
2K
RCL series circuit analysis: Damping Constant
  • · Replies 1 ·
Replies
1
Views
852