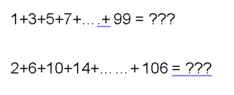Summing Formula Problem [Again]
- Context: MHB
- Thread starter susanto3311
- Start date
-
- Tags
- Formula
Click For Summary
SUMMARY
The discussion focuses on calculating the sums of two arithmetic series: the first series is the sum of odd numbers from 1 to 99, and the second series is the sum of even numbers starting from 2 to 106. The formula for the sum of an arithmetic series, \( S(n) = \frac{n}{2}[2a + (n-1)d] \), is applied to derive the sums. For the second series, with first term \( a = 2 \), common difference \( d = 4 \), and number of terms \( n = 26 \), the total sum is calculated as \( S = 1352 \).
PREREQUISITES- Understanding of arithmetic series and sequences
- Familiarity with the formula for the sum of an arithmetic series
- Basic algebra skills for manipulating equations
- Ability to identify first term, common difference, and number of terms in a series
- Explore the derivation of the arithmetic series sum formula
- Learn about geometric series and their sum formulas
- Investigate applications of arithmetic series in real-world problems
- Practice solving more complex series problems using different starting points and common differences
Students, educators, and anyone interested in mathematics, particularly those looking to enhance their understanding of series and sequences in algebra.
Similar threads
- · Replies 1 ·
- · Replies 2 ·
- · Replies 11 ·
- · Replies 4 ·
- · Replies 5 ·
- · Replies 7 ·
- · Replies 11 ·
- · Replies 9 ·
- · Replies 5 ·
- · Replies 5 ·