Super elastic collision between two objects

[noffya]

Hello,
I have difficulties with this problem:

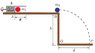
The body mass m1 = 20 g is fired with a spring, k = 72 N / m from position A. On arrival at point B hits completely elastic body mass m2 = 15 g.

Find the distance x of compressed spring so that the mass m2 reaches point C separated a distance d = 90 cm from point O. Data: h = 25 cm.

I was trying to do the calculations and camera up with these:
Since momentum P and cinetic energy are constant therefore m1*v0=m1v1+m2v2 and 1/2m1v0=1/2m1v1 +1/2m2v2
To find the v2 of the object m2 I apply conservation of energy law and it sums up to 1/2m2v2 = m2gh

After making calculations I get stuck and I think I'm missing something.
Please give an advice with this.
Thanks

 

[Doc Al]

Ask yourself: How fast must m2 have been going to land at point C?

 

[oneplusone]

Here are some useful things which I will leave for you to find (if you get stuck, ill show you how).

1. How fast does m2 have to go? (Kinematics)
2. If m2 has to go "v" meters per second, how fast would m_1 need to go right before they collide?
3. F=-kx, and F=ma, so the spring provides an acceleration to m_1 when released. How does this affect m1's speed

 

[noffya]

Here are some useful things which I will leave for you to find (if you get stuck, ill show you how).

1. How fast does m2 have to go? (Kinematics)
2. If m2 has to go "v" meters per second, how fast would m_1 need to go right before they collide?
3. F=-kx, and F=ma, so the spring provides an acceleration to m_1 when released. How does this affect m1's speed

Ask yourself: How fast must m2 have been going to land at point C?

Thanks for hints!

 

[noffya]

Here are some useful things which I will leave for you to find (if you get stuck, ill show you how).

1. How fast does m2 have to go? (Kinematics)
2. If m2 has to go "v" meters per second, how fast would m_1 need to go right before they collide?
3. F=-kx, and F=ma, so the spring provides an acceleration to m_1 when released. How does this affect m1's speed

Got it. I applied energy conservation law at step 3 and got the x equals 5.8cm
Thanks a lot!