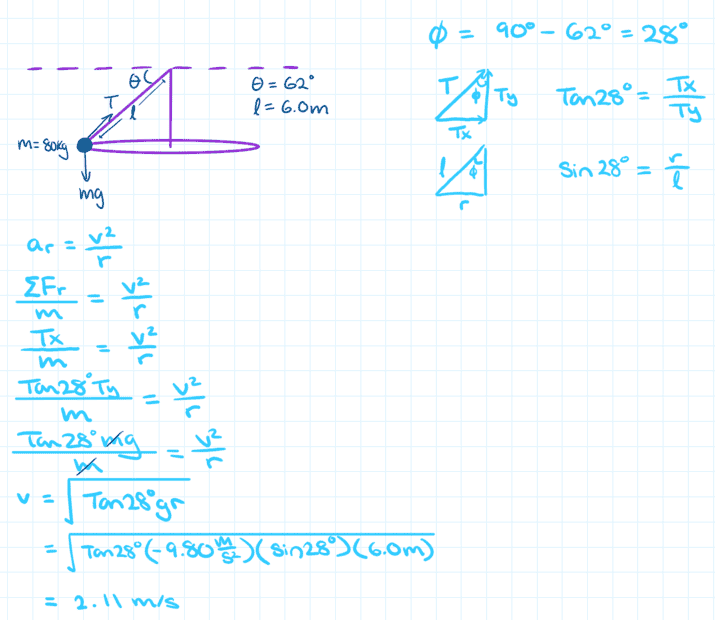Tension & Circular Motion Question - Looking for speed

[dcmf]

Homework Statement

A person sitting in a chair (combined mass 80 kg) is attached to a 6.0-m-long cable. The person moves in a horizontal circle. The cable angle θ is 62 degrees below the horizontal. What is the person's speed? Note: The radius of the circle is not 6.0 m.

Relevant Equations

a = v^2/r

I have attached a screenshot of my rough work. First of all, is my interpretation of the question correct? Please see the diagram in purple. To me, this makes sense because a=v^2/r is the only equation from my coursework that seems to relates radius (which you can find from the length of the cable) and speed.

 

[BvU]

Hello @dcmf,

​

is my interpretation of the question correct?

I guess so. Apparently the person is not in a wheelchair going around slowly ?

What do you do with the minus sign ?
And when I do the calculation, I get a different answer.

$\$

 

[Lnewqban]

Welcome, @dcmf !

All the steps seem to be correct, but the final numerical calculation is incorrect.
As Tx and Ty are directly proportional to the horizontal and vertical accelerations respectively, you could have used those values directly.

$tan~28=ac/g$

 

[dcmf]

Hi all, thank you for your replies. When you both said you're getting a different number doing the same calculation, I realized my calculator has been in radians and not degrees this entire time

Thanks for your patience and help :')

 

[BvU]

my calculator has been in radians and not degrees

Happens often (and to all of us ). Reason the more to check things, e.g. $\sin(28^\circ)\approx 0.5$ -- so you learn to smell a rat if you get $0.27$

$\$

 

[kuruman]

How did you handle the negative sign under the radical? You can't simply ignore it because it shouldn't be there. Think about this because you might will get into trouble if you replace $g$ with $-9.80~\text{m/s}^2$ indiscriminately.