Calculating Tension Force in a 3-Wire System for a 28 kg Chandelier

[kaycrew22]

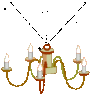
A 28 kg chandelier is suspended 1.5 m below a ceiling by three wires, each of which has the same tension and the same length of 2.0 m (see the drawing attached). Find the tension in each wire.



Equations I believe to be relevant...
W = m * g
Net force Y = T-W



So far I thought:

w = mg
w= 28kg * -9.8 m/s^2
w= 274.4 N

274.4N /3 = 91.47 N

I put this as the answer, but it says I'm wrong. Could someone please explain how this type of question is solved?

 

[LowlyPion]

Welcome to PF.

I can't see your drawing, but typically you need to break down the Tensions into the x,y components and then resolve things through solving the equations in X and Y.

 

[Dr.D]

Your tension components are each inclined, so only a part of the tension acts upward. You need to look at the geometry and figure what part of the tension component acts upward. Then also recall that you have three of those components acting to hold up the chandelier. With that, you should be able to get the force sum correct.

 

[baht_seung]

But how does the shift from in the tension vector angle translate into a fnet x vector. I have a similar problem, where two cables attach a chandelier. One is 60 degrees from the east and 40 degrees from the west.

Rather, I'm trying to find the maximum weight that the system can support if all cables have a maximum tension of 5100N.

Adding the Y components give me
5100 sin60 = 4416 lhs
5100 sin40 = 3278 rhs

 

[LowlyPion]

But how does the shift from in the tension vector angle translate into a fnet x vector. I have a similar problem, where two cables attach a chandelier. One is 60 degrees from the east and 40 degrees from the west.

Welcome to PF.

You know then for your problem that the ∑ F_x = 0

And you know also that the ∑ F_y = m*g

For x, F_x1 = T1*cos60 and F_x2 = T1*cos40

Similarly construct for the y and equate to the weight.

 

[LowlyPion]

Rather, I'm trying to find the maximum weight that the system can support if all cables have a maximum tension of 5100N.

Adding the Y components give me
5100 sin60 = 4416 lhs
5100 sin40 = 3278 rhs

That's slightly different. You need to determine first which rope is more critical to bearing maximum weight.

 

[Dr.D]

As to Kaycrew's problem, did you ever get that solved?

 

[baht_seung]

That's slightly different. You need to determine first which rope is more critical to bearing maximum weight.

$$\Sigma$$Fnet_y= 4416?

Actually there is a rope in between both that holds the chandelier

Also, how does the change in angle relate to the tensions of the strings?

Is it true to say that the more the string angle approaches 0 degrees the less

[weight] sin (theta) tension there will be?

And if this is true, how do the strings share weight?

The answer in the book says the system can hold a maximum of 6520 Newtons, however I can't seem to relate that number.

 

[LowlyPion]

Also, how does the change in angle relate to the tensions of the strings?

Because of the difference in angle you know from the horizontal that

T1*Cos40 = T2*Cos60

T1 = Cos60/Cos40 * T2

So T2 must be greater.