Tension in a string in circular motion

[Salvador_]

Homework Statement

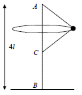
A string prq which is fixed at p and where q is vertically below p. r is a smooth ring threaded on the string which is made to rotate at an angular velocity ω rad/s in a horizontal circle centre q, the string being taut.


If |pq| = 0.12 m, |pr| + |rq| = 0.18 m,
show that ω = 294^(1/2) rad/s.

Homework Equations

m(ω^2)r

The Attempt at a Solution

I was able to solve this and get the correct answer, by setting the sum of the horizontal tension equal to the cent. force, but I had to assume that the tension in the qr part of the string is the same as the tension in the pr part. What I don't understand is how we know that the tension in both parts of the string are the same considering they are at different angles.
I was thinking that because the string is massless, it must be the same everywhere. But then I encountered another question:

For this question a ball is connected by one string (it's massless) and I had to find the tension in the lower and upper part of the string. I was able to solve this, but what's confusing me is when to know when the tension is the same everywhere in the string, and when it's different.

 

[zwierz]

is there gravity?

 

[Salvador_]

is there gravity?

Yes for both.

 

[zwierz]

As I understand the string is massless.
Then you have

Now break into the frame OXY the second Newton law: $m\boldsymbol a=\boldsymbol T_1+\boldsymbol T_2+m\boldsymbol g$

 

[Salvador_]

As I understand the string is massless.
Then you have
View attachment 205298

Now break into the frame OXY the second Newton law: $m\boldsymbol a=\boldsymbol T_1+\boldsymbol T_2+m\boldsymbol g$

I was able to solve both questions and get the correct answer. What I'm wondering is why the tension was the same for the entire string in the first question and why for the second question the tension is different in the upper and lower part.

 

[zwierz]

$|\boldsymbol T_1|$ can not be equal to $|\boldsymbol T_2|$ it is incompatible with Newton second law or with the configuration presented at the picture

 

[scottdave]

How is the ball connected? It appears that the ball physically fixed to the rope at a position on the rope. Consider an extreme case: Ask yourself, if it stops spinning so that the ball is hanging straight down, what would be the tension in the upper string? and what would be the tension in the lower string? With the ball attached at a certain point on the string, you should be able to see that the bottom string would be hanging slack, while the upper string has m*g as it's tension.
Now look at the bead which can slide around on the string. Can you see how the tension in each string would be the same when it is hanging straight down? The same works when you consider strings over pulleys.

 

[zwierz]

I guess that in case of entire string and when the bead can slide along the string freely then the triangle will not have the both sides equal

 

[Salvador_]

How is the ball connected? It appears that the ball physically fixed to the rope at a position on the rope. Consider an extreme case: Ask yourself, if it stops spinning so that the ball is hanging straight down, what would be the tension in the upper string? and what would be the tension in the lower string? With the ball attached at a certain point on the string, you should be able to see that the bottom string would be hanging slack, while the upper string has m*g as it's tension.
Now look at the bead which can slide around on the string. Can you see how the tension in each string would be the same when it is hanging straight down? The same works when you consider strings over pulleys.

I was able to follow you up to the last two lines. In the original question, the ring is traveling in a horizontal circle. qr is parallel with the ground and pr is at an angle. I'm still unsure as to how the tension is the same and how the ring is "hanging straight down".

 

[Salvador_]

$|\boldsymbol T_1|$ can not be equal to $|\boldsymbol T_2|$ it is incompatible with Newton second law or with the configuration presented at the picture

I posted two separate questions in my post. That picture applies only to the second question. The first question is a right angled triangle with a ring traveling in a horizontal circle. The only way I could get the answer 294^(1/2) was assuming that the tensions were the same.

 

[scottdave]

I was able to follow you up to the last two lines. In the original question, the ring is traveling in a horizontal circle. qr is parallel with the ground and pr is at an angle. I'm still unsure as to how the tension is the same and how the ring is "hanging straight down".

Actually, I was referring to "if the pole stops spinning, what will happen to the bead?" Will it stay in the same place on the line, or will it slide down? The problem statement indicates that it can slide. With the pole stopped, it will hang straight down. What is the tension in the "two" strings (actually the same string). Now if the pole is spinning, you can expect the bead to slide up, and the tension on either side of the bead will be equal magnitude.

 

[scottdave]

With the sliding bead, you should expect the tensions to be equal magnitude. If the bead were tied off, unable to slide, then the tensions will under most circumstances not be the same. I was demonstrating an extreme case of the pole stopping, to show how in the sliding bead, the tension remains the same on either side, while in the fixed ball, they are not.

 

[Salvador_]

With the sliding bead, you should expect the tensions to be equal magnitude. If the bead were tied off, unable to slide, then the tensions will under most circumstances not be the same. I was demonstrating an extreme case of the pole stopping, to show how in the sliding bead, the tension remains the same on either side, while in the fixed ball, they are not.

How are the tensions equal in magnitude when the bead is sliding, shouldn't the upper string have more tension because of the gravity on the bead?

 

[scottdave]

Let's say the pole is not moving. So the bead hangs straight down, and each side of the string has a tension of (m*g)/2. As it starts spinning, you will have a horizontal component (m*a). This will increase as the pole spins faster. Each side of the string has the same magnitude of tension, but in different directions: each one carries a different portion of the horizontal and vertical components.

 

[Salvador_]

Let's say the pole is not moving. So the bead hangs straight down, and each side of the string has a tension of (m*g)/2. As it starts spinning, you will have a horizontal component (m*a). This will increase as the pole spins faster. Each side of the string has the same magnitude of tension, but in different directions: each one carries a different portion of the horizontal and vertical components.

Yes I kind of understand it better now. Thanks!

 

[haruspex]

Yes I kind of understand it better now. Thanks!

For what it's worth, here's how I would answer your question.
Consider a very small section of string in contact with the ring around a short arc. It is acted on by three forces, the two tensions from neighbouring sections and the normal force from the ring. There is no friction. The two tensions form the same angle to the normal force. It is easy to show this means they must be equal.