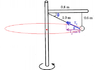
SUMMARY
The discussion clarifies the relationship between tension and centripetal force in circular motion, specifically addressing the derivation of T2cos(theta) as the centripetal force. The centripetal force is defined as Fc = mv^2/R, where T2cos(theta) represents the horizontal component of the tension in rope 2 acting on an object moving in a horizontal circle. The confusion arises from equating the tension directly with the centripetal force, but it is established that the x-component of T2 is indeed the centripetal force required to maintain circular motion.
PREREQUISITES
- Understanding of circular motion dynamics
- Familiarity with tension in ropes and forces
- Knowledge of trigonometric functions, particularly cosine
- Basic physics equations related to centripetal force
NEXT STEPS
- Study the derivation of centripetal force equations in detail
- Explore the role of tension in different types of circular motion
- Learn about the application of trigonometric functions in physics problems
- Investigate real-world examples of circular motion and tension forces
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, educators teaching circular motion concepts, and anyone seeking to understand the dynamics of forces in circular motion scenarios.