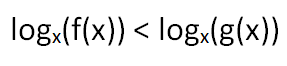The Limited Logarithm: Why x Can't Be <= 0
- Context: MHB
- Thread starter roni1
- Start date
-
- Tags
- Logarithm
Click For Summary
SUMMARY
The discussion clarifies that logarithms are only defined for positive bases due to the mathematical implications of exponentiation. Specifically, the equation P = log_x(Q) translates to Q = x^P, which presents undefined scenarios when x is less than or equal to zero. For instance, defining x^{-1} when x equals 0 or x^{1/2} when x equals -1 leads to contradictions, necessitating the restriction of logarithmic functions to positive bases only.
PREREQUISITES- Understanding of logarithmic functions
- Familiarity with exponentiation principles
- Basic knowledge of mathematical definitions and properties
- Concept of undefined mathematical expressions
- Study the properties of logarithms with positive bases
- Explore the implications of exponentiation with negative and zero bases
- Learn about complex logarithms and their definitions
- Investigate mathematical conventions for undefined expressions
Mathematicians, educators, students studying algebra, and anyone interested in the foundational principles of logarithmic functions.
Similar threads
High School
Issue With Algebra of Logarithms
- · Replies 8 ·
- · Replies 11 ·
- · Replies 5 ·
- · Replies 12 ·
- · Replies 17 ·
- · Replies 17 ·
- · Replies 2 ·
- · Replies 4 ·
- · Replies 5 ·