The Two Child Problem (revisited)

[BenVitale]

See article in Wikipedia

And, Column By John Allen Paulos

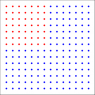
Scenario 1: A woman has two children, the older of whom is a boy. Given this knowledge, what is the probability that she has two boys?

No problem here, the answer is 1/2

Scenario 2: Assume that you know that a woman has two children, at least one of whom is a boy. You know nothing about this boy except his sex. Given this knowledge, what is the probability that she has two boys?

We have come to accept that the probability the woman has two boys is 1/3, not 1/2.

Here's the kicker:

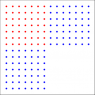
Suppose that when children are born in a certain large city, the season of their birth, whether spring, summer, fall, or winter, is noted prominently on their birth certificate. The question is: Assume you know that a lifetime resident of the city has two children, at least one of whom is a boy born in summer. Given this knowledge, what is the probability she has two boys?

This appears to be essentially the same as the scenario 2. But instead, they would find that 7/15 of these women have two boys.

An increase in probability from 1/3 to 7/15 !

Doesn't this change in probability seem strange?

I got a bit confused after reading the following problem:

I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?

Answer: the probability of two boys is 13/27

Source: http://alexbellos.com/?p=725

 

[bpet]

... Here's the kicker ...

Nice twist on an old paradox!

Sometimes a diagram helps. The sample space for the day of week version can be visualized on a 14 x 14 grid with the conditional probabilities just being the proportion of red dots (see below).

 

[BenVitale]

bpet,

Thanks. The diagram helps.

So, going back to John Allen Paulos, in the Summer the probability of having boys is higher.
I wonder how did Paulos compute that?

I was looking on the web for seasonal distribution of births of boys, but couldn't find anything. Have you searched for any stats?

All I know is, the ratio of males to females in a population is 107 boys to 100 girls or 105 boys to 100 girls (Fisherian sex ratio), but it's not always the case because of the ratios may be considerably skewed due to abortion, infant mortality, etc.

 

[bpet]

...So, going back to John Allen Paulos, in the Summer the probability of having boys is higher.
I wonder how did Paulos compute that? ...

I thought he was saying the opposite, namely that observing a higher proportion of boys among families with a boy born in summer, does NOT imply that the summer birth ratio is higher. Also, if you want to know where the 7/15 came from, it can be computed by drawing an 8x8 grid similar to the one above.

 

[blue_raver22]

I would first like to clarify that the question about the Two Child Problem is a hypothetical scenario and not a real-life situation. In real-life, the probability of having two boys is always 1/2, regardless of any other information.

In the first scenario, the probability of having two boys is indeed 1/2, as there are only two possible outcomes - two boys or one boy and one girl. This is a basic principle of probability - the number of favorable outcomes divided by the total number of outcomes.

In the second scenario, the probability of having two boys is 1/3, as there are three possible outcomes - two boys, two girls, or one boy and one girl. However, this scenario assumes that the woman has at least one boy, which eliminates the possibility of two girls. This is known as the "Boy or Girl" problem and the answer is 1/3.

In the third scenario, the probability of having two boys is indeed 7/15, which may seem strange at first. However, this scenario introduces an additional factor - the season of birth. This means that the total number of possible outcomes is not just three (two boys, two girls, or one boy and one girl), but four (two boys born in different seasons, one boy born in summer, and one boy born in any other season). This changes the probability to 7/15.

The problem with the Tuesday-born boy is a similar scenario, where an additional factor (the day of birth) is introduced. This changes the total number of possible outcomes to 27 (two boys born on different days, one boy born on Tuesday, and one boy born on any other day). This gives a probability of 13/27.

In conclusion, the change in probability may seem strange, but it is a result of introducing additional factors or conditions that affect the total number of possible outcomes. As scientists, we must always carefully consider all factors and conditions when calculating probabilities to ensure accurate results.