A The vertex factors in QCD penguin operators

Click For Summary
The discussion centers on the presence of a (V+A) term in QCD penguin operators, specifically in O5 and O6. Participants question why this term exists when electroweak theory typically assigns a (V-A) factor to Dirac spinor-W boson vertices, as W bosons couple only to left Weyl spinors. The conversation highlights the need for clarity on what is being calculated to understand the inclusion of the (V+A) term. One participant acknowledges the confusion but later expresses that the issue is now clear. The dialogue emphasizes the importance of context in theoretical calculations.
Elmo
Messages
37
Reaction score
6
TL;DR
Not sure why there is a (V+A) term in here.
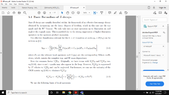
Have a look at O5 & O6 in Eqtns(5.4) . Why is there a (V+A) ?
(V+A) contains the projection operator which projects out the right Weyl from a Dirac spinor.
As per the Feynman rules of electroweak theory, there is a (V-A) assigned to each (Dirac) spinor-W boson vertex because W only couple to left Weyl spinors.
In the corresponding penguin diagrams there is the quark-antiquark loop coupling to the W so shouldn't both vertices have the same (V-A) factor always ?
Screenshot (51).png
 
Physics news on Phys.org
Elmo said:
Summary:: Not sure why there is a (V+A) term in here.

so shouldn't both vertices have the same (V-A) factor always ?

Maybe. You didn't post enough for us to see what is being calculated. We therefore can't tell what should or should not be there.
 
Vanadium 50 said:
Maybe. You didn't post enough for us to see what is being calculated. We therefore can't tell what should or should not be there.
oh sorry.np Here it is.
 

Attachments

  • Screenshot (53).png
    Screenshot (53).png
    51.5 KB · Views: 207
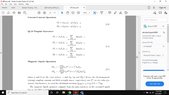
  • Screenshot (54).png
    Screenshot (54).png
    43.5 KB · Views: 204
  • Screenshot (55).png
    Screenshot (55).png
    40 KB · Views: 188
You still haven't shown us what is being calculated. Why this slow drip...drip..drip of information?

If the goal is, for example, to put constraints on a potential V+A interaction or component, of course it needs to be there.
 
Vanadium 50 said:
You still haven't shown us what is being calculated. Why this slow drip...drip..drip of information?

If the goal is, for example, to put constraints on a potential V+A interaction or component, of course it needs to be there.
oh actually no,I think its all clear now.
Sorry for bugging ye all.
Thanks anyway.
 
Thread 'Some confusion with the Binding Energy graph of atoms'

Thread 'Some confusion with the Binding Energy graph of atoms'

My question is about the following graph: I keep on reading that fusing atoms up until Fe-56 doesn’t cost energy and only releases binding energy. However, I understood that fusing atoms also require energy to overcome the positive charges of the protons. Where does that energy go after fusion? Does it go into the mass of the newly fused atom, escape as heat or is the released binding energy shown in the graph actually the net energy after subtracting the required fusion energy? I...
View full post »

Similar threads

A Operator Product Expansion as shown in Schwartz
Replies
4
Views
2K
A The Factorization Theorem in Particle Physics
Replies
6
Views
2K
A How the g factor comes from QFT?
Replies
1
Views
2K
I The standard model from loop quantum gravity via spinors octonions
Replies
26
Views
5K
I Progress In Calculating The HLbL Contribution To Muon g-2
Replies
0
Views
2K
Conformal field theory: vertex operator
Replies
11
Views
3K
What is the Role and Significance of Feynman Diagrams in Quantum Physics?
Replies
1
Views
2K
New properties of "standard model effective field theory"
Replies
7
Views
3K
How to Renormalize Non-Local Quantum Field Theory?
Replies
2
Views
2K
I Muon g-2 as a constraint on new physics
Replies
18
Views
4K