The Von Mises stress equation on wikipedia does not balance out

[FQVBSina_Jesse]

TL;DR

The Von Mises stress relationship on Wikipedia shows an expanded expression using components is equal to 3/2*s_ij*s_ij but this is not possible.

On Wikipedia for Von Mises stress, it shows the following equation:

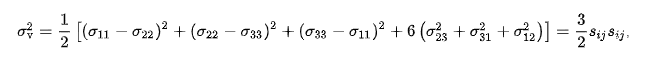
But this does not work out. If I expand the second term I get:

$$ \sigma_v^2 = 1/2[(\sigma_{11}^2-2\sigma_{11}\sigma_{22}+\sigma_{22}^2+\sigma_{22}^2-2\sigma_{22}\sigma_{33}+\sigma_{33}^2+\sigma_{33}^2-2\sigma_{33}\sigma_{11}+\sigma_{11}^2)+6(\sigma_{12}^2+\sigma_{13}^2+\sigma_{23}^2)] $$

$$ \sigma_v^2 = 1/2(2\sigma_{11}^2 + 2\sigma_{22}^2+2\sigma_{33}^2-2\sigma_{11}\sigma_{22}-2\sigma_{22}\sigma_{33}-2\sigma_{33}\sigma_{11}+6\sigma_{12}^2+6\sigma_{13}^2+6\sigma_{23}^2) $$

$$ \sigma_v^2 = \sigma_{11}^2 + \sigma_{22}^2+\sigma_{33}^2-\sigma_{11}\sigma_{22}-\sigma_{22}\sigma_{33}-\sigma_{33}\sigma_{11}+3\sigma_{12}^2+3\sigma_{13}^2+3\sigma_{23}^2 $$

And I don't see how this can be equal to the third term, when expanded equals to:

$$ 3/2s_{ij}s_{ij} = 3/2(\sigma_{11}^2+\sigma_{22}^2+\sigma_{33}^2+\sigma_{12}^2+\sigma_{13}^2+\sigma_{23}^2) $$

 

[Frabjous]

Not in a good place to look at this, but I believe s is deviatoric stress.

 

[FQVBSina_Jesse]

Not in a good place to look at this, but I believe s is deviatoric stress.

You are correct! But then, what is the definition of the following?

$$SVM = sqrt(3/2*\sigma_{ij}*\sigma_{ij})$$

sigma is stress. Previously I thought Svm is Von Mises Stress, but now it might be deviatoric stress, s. Then I am not sure what SVM defined as such is supposed to be.

 

[Frabjous]

s_ij=σ_ij-(σ_kk/3)δ_ij
Both s and σ appear in the equation