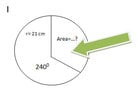
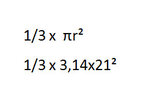This is known as the Sector Area Formula.
Click For Summary
SUMMARY
The discussion focuses on deriving the area of a circular sector using the angle subtended at the center. Specifically, if the angle is $240^{\circ}$, the remaining angle within the sector is $120^{\circ}$. This leads to the conclusion that the area of the sector can be calculated as a fraction of the total area of the circle. The formula established is $A=\frac{1}{2}\theta r^2$, where $\theta$ is in radians and $r$ is the radius of the circle.
PREREQUISITES- Understanding of circular geometry
- Familiarity with radians and degrees
- Basic knowledge of area calculations
- Ability to manipulate algebraic formulas
- Study the relationship between degrees and radians in circular measurements
- Learn how to derive the area of a circle using the formula $A=\pi r^2$
- Explore applications of the sector area formula in real-world problems
- Investigate the implications of sector areas in trigonometry
Students studying geometry, educators teaching circular measurements, and anyone interested in mathematical problem-solving related to areas of circles and sectors.
Similar threads
- · Replies 4 ·
- · Replies 8 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 5 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 3 ·