rdn98
- 39
- 0
I've included a picture.
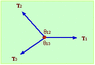
Three strings, in the horizontal plane, meet in a knot and are pulled with three forces such that the knot is held stationary. The tension in string 1 is T1 = 3.6 N. The angle between strings 1 and 2 is 130° and the angle between strings 1 and 3 120° with string 3 below string 1 as shown.
a) Find the tension in string 2.
b) Find the tension in string 3.
-----------------------------------------
A mass of 2.1 kg is now placed on the knot and supported by a frictionless table in the plane of the strings.
------------------------------------------------
c) Find the acceleration of the mass if all the forces remain the same as above.
d) If the sizes and directions of T2 and T3 remain the same, but T1 is increased by 1.5 N, what is the acceleration of the mass?
================================================================
Okay. I'm having trouble finding the tensions of string 2 and 3. I did split up both vectors into their components, but I tried out some trig and its not working for me.
For string 2, I tried T2= 3.6/(cos 50). That doesn't work.
For string 3, I tried T3= 3.6/(cos 240). That didn't work either.
From the hints, I'm supposed to have two equations and two unknowns, but I don't know how to derive these equations.
If I can do these two, then hopefully I can do the rest of the problem.
Three strings, in the horizontal plane, meet in a knot and are pulled with three forces such that the knot is held stationary. The tension in string 1 is T1 = 3.6 N. The angle between strings 1 and 2 is 130° and the angle between strings 1 and 3 120° with string 3 below string 1 as shown.
a) Find the tension in string 2.
b) Find the tension in string 3.
-----------------------------------------
A mass of 2.1 kg is now placed on the knot and supported by a frictionless table in the plane of the strings.
------------------------------------------------
c) Find the acceleration of the mass if all the forces remain the same as above.
d) If the sizes and directions of T2 and T3 remain the same, but T1 is increased by 1.5 N, what is the acceleration of the mass?
================================================================
Okay. I'm having trouble finding the tensions of string 2 and 3. I did split up both vectors into their components, but I tried out some trig and its not working for me.
For string 2, I tried T2= 3.6/(cos 50). That doesn't work.
For string 3, I tried T3= 3.6/(cos 240). That didn't work either.
From the hints, I'm supposed to have two equations and two unknowns, but I don't know how to derive these equations.
If I can do these two, then hopefully I can do the rest of the problem.