Time Series: stationary AR(1) -> MA(infinity)

[kingwinner]

Theorem:
A stationary AR(1) model can be expressed in terms of MA(infinity).

Proof:

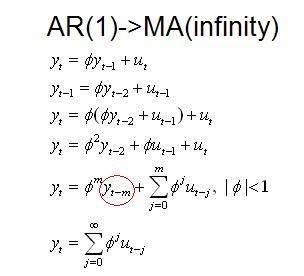
Now I don't understand how they get from the second last line to the last line. Where did the term Y_t-m go?

I understand you can keep doing the substitution iteratively, but you always have to end up with a "Y" term no matter how many times you do it, but on the last line of the proof there is no "Y" term, so it magically disappared? I'm really confused.

Hopefully someone can explain this (in simple terms if possible). Thank you!

 

[pmsrw3]

They're taking the limit as \phi goes to infinity. What happens to \phi^m in that limit?

 

[kingwinner]

I think it's the limit as m->∞.

As m->∞,
φ^m ->0
BUT you also have to look at what happens to the other term, right? What if Y_t-m->∞? Then we have indeterminate form 0*∞, and we just can't conclude that the product->0.
(Also, another complication is that Y_t-m is a random variable, so I'm not sure if all of these make sense or not.)

 

[pmsrw3]

I think it's the limit as m->∞.

You're right -- sorry.

As m->∞,
φ^m ->0
BUT you also have to look at what happens to the other term, right? What if Y_t-m->∞? Then we have indeterminate form 0*∞, and we just can't conclude that the product->0.

(Also, another complication is that Y_t-m is a random variable, so I'm not sure if all of these make sense or not.)

I'll take those two complications in reverse order. First, the equation will in general be true "almost surely", meaning with probability 1. It may be possible for \phi^m y_{t-m} to approach a constant or diverge, but this happens with probability 0. Second, you have to know SOMETHING about the y's. If this is the same book that your random walk problem came from, maybe they left out essential information. But the key fact is there in the word "stationary". It takes a little work to prove it, but If y is a decently-behaved RV (i.e., has a CDF) and is stationary and |\phi|<1, then \lim_{m\to\infty}\phi^m y_{t-m}=0 almost surely.