To find the time taken for one vessel to reach another

[gnits]

Homework Statement

To find the time taken for one vessel to reach another

Relevant Equations

d=st

Could I please ask for help regarding my answer to the following question?

I've done the first part and get the answer of 500 seconds.

I anticipated no problem with the second part, it is the same problem with different inputs, but I have disagreed with the provided answer of 1754 seconds. I get 1283 seconds. My method for this part is the same as for the first.

My reasoning was that after the 500 seconds has elapsed, A will have moved on a further 8 * 500 = 4000 metres and B will have moved on a further 10 * 500 = 5000 metres and the starting position will be as in the diagram below:

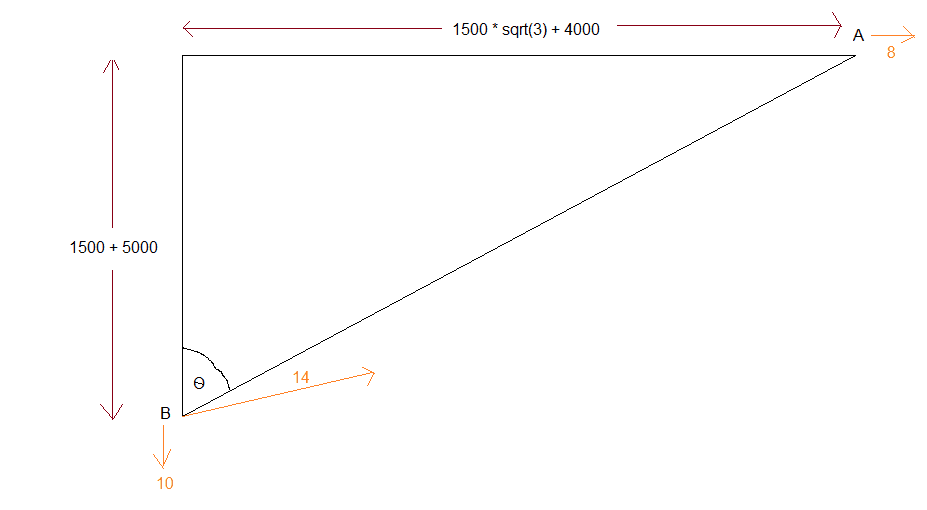
So the angle $\theta$ is given by $atan(\frac{1500\sqrt{3}+4000}{6500}) = 45.43^\circ$

Let the speed of the motor boat in the northerly direction (i) be $M_x$ and in the easterly direction (j) be $M_y$, we know that $M_x^2+M_y^2=14^2=196$

Finally, let $V_{MA}=V_M-V_A$ be the velocity of the motor boat relative to A. Then we have:

$V_{MA}=(M_x-8)\,i + M_y\,j$

Now, in order to intercept A, $V_{MA}$ must be parallel to the initial displacement of A from B. Thus we have (for a certain scalar K):

$(M_x-8)\,i + M_y\,j\,=\,sin(45.43^\circ)K\,i + cos(45.43^\circ)K\,j$

so

$(M_x-8)\,i + M_y\,j\,=\,0.7124K\,i + 0.7018K\,j$

And so $M_x-8=0.7124K$

and $M_y = 0.7018K$

which gives:

$(0.7124K+8)^2+(0.7018K)^2=196$

This is solved for K, I take positive root to give correct direction of travel parallel tp AB of K = 7.12574 and this leads to:

$M_y=0.7018*7.12574=5.065$

And so time taken to reach A is $6500/5.065=1283$

Thanks for any help,
Mitch.

 

[mjc123]

I agree with your answer. 1754 s corresponds to a speed of 12.33 m/s.

 

[gnits]

Thanks for checking. The verification is important. Without it, it feels wrong to just assume the books answer incorrect. Mitch.

 

[PeroK]

Thanks for checking. The verification is important. Without it, it feels wrong to just assume the books answer incorrect. Mitch.

The $1754s$ could be the total time. Although, I actually get an answer of $1300s$ for the return journey.

The numbers in this problem defeated me, so I retreated into the sanctuary of algebra and got:
$$ t = \frac{1}{v^2 - u^2}(lu + \sqrt{(lu)^2 + d^2(v^2 - u^2)})$$
Where $v$ is the speed of the motor boat, $u$ the speed of the boat it's chasing; $d$ is the initial total distance between the motor boat and the target and $l$ is the initial distance in the direction of $u$.