To find the tipping point of a lamina

[gnits]

Homework Statement

To find the tipping point of a lamina

Relevant Equations

Balance of torques

Could I please ask for help with the following:

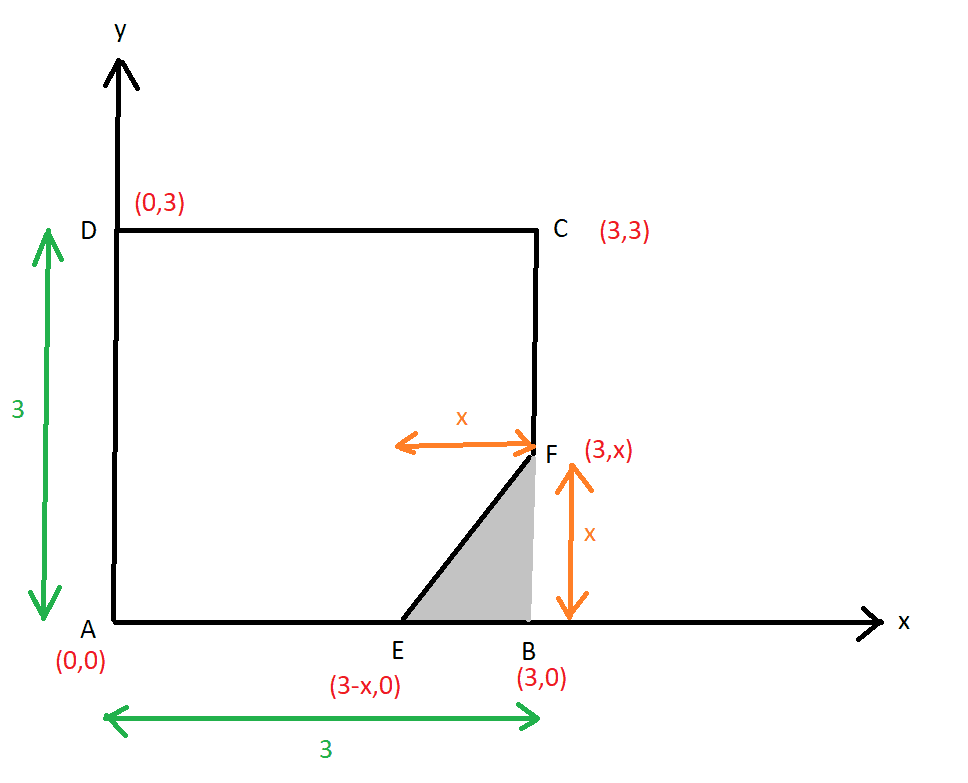
ABCD is a uniform square metal plate of side 3m. Points E and F are taken on AB and BC respectively such that BE = BF = x m and the portion BEF is removed.

1) Find the distance of the centroid of the remainder from AD

2) Show that the remainder cannot stand in equilibrium on AE with AD vertical unless 2x^3-54x+81 >= 0

3) If the mass of the remainder is 14kg, find in Newtons the least horizontal force applied at C required to maintain it in equilibrium in this position when x = 2.

Here's a diagram:

1) I believe I'm ok with this part. Let w = weight per unit area of lamina.

Weight of ABCD is 9w
Weight of BEF is (1/2)x^2w
Weight of AEFCD is therefore ( 9 - (1/2)x^2 )w

Distance of COG of ABCD from AD is 3/2
Distance of COG of BED from AD is (3-x+3 + 3) / 3 = (9-x)/3

Equating moments of these parts about AD gives:

9w * (3/2) + (1/2)x^2w * (9-x)/3 = (9 - (1/2)x^2)w * X

where X is the x-ordinate of the centre of gravity = distance of centroid from AD

This solves to give X = (81 - x^2(9-x)) / 3(18-x^2)

2) Given the above answer I would have said that the condition for the remainder to stand in equilibrium with AD vertical would be that X <= 3 - x otherwise the C.O.G. would be to the right of E. So this leads to (81 - x^2(9-x)) / 3(18-x^2) <= x - 3 which (using Wolfram Alpha for speed of checking) leads to x >= 9/2. Not the required answer.

3) OK with this part and it gives me confidence in my answer to part 1 because I get the book answer of 12.2N.

Here we are told that x = 2, and so E is at 3 - 2 = 1. From the above formula we get that X is at 53/42 and so overhangs E by 53/42 - 1 = 11/42. So with a force f acting at C to preserve equilibrium we can say that moments about E should by zero. Force down is 14g = 14 * 10 Newtons . This leads to:

14 * 10 * (11/42) + f * 3 = 0

Which solves to give f = 12.2 Newtons.

Thanks for any help with part 2.

Mitch.

 

[Steve4Physics]

2) Given the above answer I would have said that the condition for the remainder to stand in equilibrium with AD vertical would be that X <= 3 - x otherwise the C.O.G. would be to the right of E. So this leads to (81 - x^2(9-x)) / 3(18-x^2) <= x - 3 which (using Wolfram Alpha for speed of checking) leads to x >= 9/2. Not the required answer.

"(81 - x^2(9-x)) / 3(18-x^2) <= x - 3"
should be
(81 - x^2(9-x)) / 3(18-x^2) <= 3 - x

Other thoughts...

x= 9/2 (m) clearly can't be correct because the maximum possible value of x is 3m (as you probably already realize).

The question only asks you to show $2x^3 - 54x+81 ≥ 0$, not to determine the ‘critical value’ of x. So you are not asked to solve $2x^3 - 54x+81 = 0$. You just need to simplify$$\frac {81 – x^2(9-x)} {3(18-x^2)} ≤ 3-x$$to show it gives the required inequality.

 

[gnits]

"(81 - x^2(9-x)) / 3(18-x^2) <= x - 3"
should be
(81 - x^2(9-x)) / 3(18-x^2) <= 3 - x

Other thoughts...

x= 9/2 (m) clearly can't be correct because the maximum possible value of x is 3m (as you probably already realize).

The question only asks you to show $2x^3 - 54x+81 ≥ 0$, not to determine the ‘critical value’ of x. So you are not asked to solve $2x^3 - 54x+81 = 0$. You just need to simplify$$\frac {81 – x^2(9-x)} {3(18-x^2)} ≤ 3-x$$to show it gives the required inequality.

Thanks very much. Massive help. I see it now.
Mitch.