To prove that Cauchy sequence

[ozkan12]

View attachment 4866View attachment 4867View attachment 4868View attachment 4859View attachment 4860View attachment 4861View attachment 4862View attachment 4863View attachment 4864View attachment 4865View attachment 4869

My Questions:

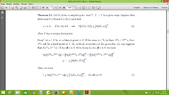
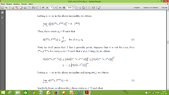
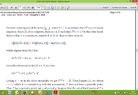
1) İn both sides of inequality of (*) why we use "n", that is, why we do multiplication with "n" ?

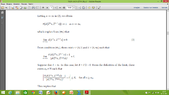
2) in (**) by Letting $n\to\infty$ we obtain $\lim_{{n}\to{\infty}} n\left[d\left({T}^{n}x,{T}^{n+1}x\right)\right]{}^{r}=0$ How this happened ?

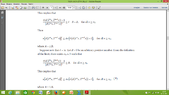
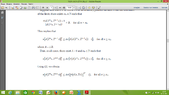
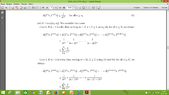
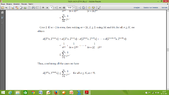
3) Since, $\lim_{{n}\to{\infty}} n\left[d\left({T}^{n}x,{T}^{n+1}x\right)\right]{}^{r}=0$ there exists ${n}_{1}\in\Bbb{N}$ such that $d\left({T}^{n}x, {T}^{n+1}x\right)\le\frac{1}{{n}^{\frac{1}{r}}}$... How we can write this ?
Also, why we use number $\frac{1}{{n}^{\frac{1}{r}}}$ ?

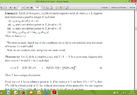
Please can you give an answer to my questions ? Thank you for your attention..

 

[Ackbach]

My Questions:

1) İn both sides of inequality of (*) why we use "n", that is, why we do multiplication with "n" ?

2) in (**) by Letting $n\to\infty$ we obtain $\lim_{{n}\to{\infty}} n\left[d\left({T}^{n}x,{T}^{n+1}x\right)\right]{}^{r}=0$ How this happened ?

I'm not at all sure I buy it, myself. It's not clear at all from, say, the $(\Theta_3)$ condition that $\theta^{k^n}$ goes to $1$ faster than $n\to\infty$, which is certainly what you'd need to conclude (**). I could buy, from the $(\Theta_3)$ condition, that
$$\lim_{n\to\infty}n^r \left(\theta^{n^k}-1\right)=\ell,$$
where $0<r<1$, but as we don't seem to have much control over the size of $\ell$, I'm not sure that helps us much.

Hang on: I think it might be a typo. I think you could conclude that IF:
$$\lim_{n\to\infty}[d(T^nx,T^{n+1}x)]^r=0,$$
THEN there exists an $n_1>0$ such that for all $n>n_1$, you have
$$d(T^nx,T^{n+1}x)\le \frac{1}{n^{1/r}}.$$
Isn't that pretty close to the definition of convergence? Our $\varepsilon$ is just written in this fancy way. I could be wrong, but I think this works.

3) Since, $\lim_{{n}\to{\infty}} n\left[d\left({T}^{n}x,{T}^{n+1}x\right)\right]{}^{r}=0$ there exists ${n}_{1}\in\Bbb{N}$ such that $d\left({T}^{n}x, {T}^{n+1}x\right)\le\frac{1}{{n}^{\frac{1}{r}}}$... How we can write this ?
Also, why we use number $\frac{1}{{n}^{\frac{1}{r}}}$ ?

Please can you give an answer to my questions ? Thank you for your attention..

I think the author wants to be able to do the sums at the very end of the proof, and this form of $\varepsilon$ let's him do that.

 

[ozkan12]

Dear Ackbach

İn your post, I think these definitions close to definition of convergence but this carry very special conditions...But I didnt understand why we choose $\varepsilon$ in this way ? Because this is very special, I think that can we take $\varepsilon$ different from this ? This article is hard for me :)