nanuba said:
I've started f(T) theory but I have a simple question like something that i couldn't see straightforwardly.
In Teleparallel theories one has the torsion scalar:
View attachment 85890
View attachment 85891
And if you take the product you should obtain
View attachment 85892
But there seems to be the terms like
View attachment 85893View attachment 85894View attachment 85895.
How does this one vanish?
because we know that Torsion tensor is not symmetric in first two indices but antisymmetric in the last two indices.
Will you buy me strong black coffee if I do it for you? Okay, start by multiplying the two tensor
S^{\rho\mu\nu}T_{\rho\mu\nu} = A + B , \ \ \ \ \ (1)
where
A = \frac{1}{4} T^{\rho\mu\nu}T_{\rho\mu\nu} + \frac{1}{4} T^{\mu\rho\nu}T_{\rho\mu\nu} - \frac{1}{4} T^{\nu\rho\mu}T_{\rho\mu\nu} , \ \ \ \ (2) and B = -\frac{1}{2}T_{\alpha}{}^{\mu\alpha} \ T^{\rho}{}_{\mu\rho} + \frac{1}{2}T_{\alpha}{}^{\nu\alpha} \ T^{\rho}{}_{\rho\nu} , or
B = -\frac{1}{2}T_{\alpha}{}^{\mu\alpha} \ T^{\rho}{}_{\mu\rho} - \frac{1}{2}T_{\alpha}{}^{\mu\alpha} \ T^{\rho}{}_{\mu\rho} = - T_{\alpha}{}^{\mu\alpha} \ T^{\rho}{}_{\mu\rho} , which is the same as
B = T_{\alpha}{}^{\mu\alpha} \ T^{\rho}{}_{\rho\mu} = T^{\alpha\mu}{}_{\alpha} \ T^{\rho}{}_{\rho\mu} . \ \ \ \ \ (3) That is all for B. To work on A, we start with the identity
T^{\mu\nu}{}_{\rho} \left( T^{\rho}{}_{\nu\mu} + T^{\rho}{}_{\mu\nu} \right) = 0 . In the first term, if we make \rho \to \nu, \mu \to \rho and \nu \to \mu, we find
T^{\rho\mu}{}_{\nu} \ T^{\nu}{}_{\mu\rho} + T^{\mu\nu}{}_{\rho} \ T^{\rho}{}_{\mu\nu} = 0 . Let us rewrite this as
T^{\rho\mu\nu} \ T_{\nu\mu\rho} + T_{\mu\nu\rho} \ T^{\rho\mu\nu} = 0 . Using the antisymmetry in the second term, we get
T^{\rho\mu\nu} \ T_{\nu\mu\rho} = T^{\rho\mu\nu} \ T_{\mu\rho\nu} . Now, on the RHS we make \rho \leftrightarrow \mu and get
T^{\rho\mu\nu} \ T_{\nu\mu\rho} = T^{\mu\rho\nu} \ T_{\rho\mu\nu} . Add T^{\rho\mu\nu}T_{\nu\mu\rho} to both sides,
T^{\rho\mu\nu} \ T_{\nu\mu\rho} = \frac{1}{2}\left( T^{\mu\rho\nu} \ T_{\rho\mu\nu} + T^{\rho\mu\nu} \ T_{\nu\mu\rho} \right) . In the second term on the RHS, lower the indices on the first tensor and raise them on the second tensor
T^{\rho\mu\nu} \ T_{\nu\mu\rho} = \frac{1}{2}\left( T^{\mu\rho\nu} \ T_{\rho\mu\nu} + T_{\rho\mu\nu} \ T^{\nu\mu\rho} \right) . Using the antisymmetry and dividing by 2, we obtain
\frac{1}{4} T^{\mu\rho\nu} T_{\rho\mu\nu} - \frac{1}{4} T^{\nu\rho\mu} T_{\rho\mu\nu} = \frac{1}{2} T^{\rho\mu\nu}T_{\nu\mu\rho} = - \frac{1}{2} T^{\rho\mu\nu} T_{\nu\rho\mu}. And finally, we rewrite this identity in the form
\frac{1}{4} T^{\mu\rho\nu} T_{\rho\mu\nu} - \frac{1}{4} T^{\nu\rho\mu} T_{\rho\mu\nu} = - \frac{1}{2} T^{\rho\mu}{}_{\nu} \ T^{\nu}{}_{\rho\mu} . Now, substituting this identity in (2) leads to A = \frac{1}{4} T^{\rho\mu\nu} T_{\rho\mu\nu} - \frac{1}{2} T^{\rho\mu}{}_{\nu} \ T^{\nu}{}_{\rho\mu} . \ \ \ (4) Now, put (3) and (4) in (1), you get
S^{\rho\mu\nu}T_{\rho\mu\nu} = \frac{1}{4} T^{\rho\mu\nu} T_{\rho\mu\nu} - \frac{1}{2} T^{\rho\mu}{}_{\nu} \ T^{\nu}{}_{\rho\mu} + T^{\alpha\mu}{}_{\alpha} \ T^{\rho}{}_{\rho\mu} .
Okay, don’t forget my coffee.
Sam
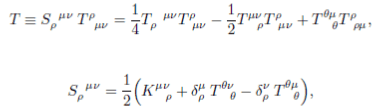
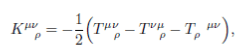
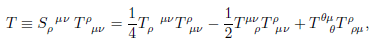
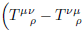
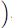
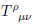 .
.