Tractrix on a line below the x-axis

[Dr Edward]

The cusp of the tractrix is on the y-axis.
I have been studying Sreenavisan et al (Mechanism and Machine Theory 45 (2010) 454–466)
Email me for copy, if needed.
What I need is the equation of a tractrix with the hitch point not on the x-axis but on a line below (y=-mx).
Any help would be gratefully received.
Dr Edward

 

[I like Serena]

The cusp of the tractrix is on the y-axis.
I have been studying Sreenavisan et al (Mechanism and Machine Theory 45 (2010) 454–466)
Email me for copy, if needed.
What I need is the equation of a tractrix with the hitch point not on the x-axis but on a line below (y=-mx).
Any help would be gratefully received.
Dr Edward

Hello Dr Edward and welcome to MHB! ;)

We can move a graph vertically by replacing every occurrence of $y$ by $y-b$.
The result is shifting the graphs upwards by $b$.
Similarly we can shift a graph horizontally by replacing every occurrence of $x$ by $x-a$.

 

[Dr Edward]

Thank you very much. That is indeed helpful.
Here is an excerpt from SreenavisanView attachment 8556
In all his brilliance he makes the integrating task like getting an ice cream.
I tried MathCad and the result was kilometres long.
My knowledge of maths is not that good to simplify.
I need an equation y=f(x) or y=f(t).
Hope you can help
Cheers
Edward

 

[I like Serena]

Thank you very much. That is indeed helpful.
Here is an excerpt from Sreenavisan
In all his brilliance he makes the integrating task like getting an ice cream.
I tried MathCad and the result was kilometres long.
My knowledge of maths is not that good to simplify.
I need an equation y=f(x) or y=f(t).
Hope you can help
Cheers
Edward

I kind of doubt that Sreenavisan has a nice simple formula in the form $y=f(x)$.
Instead I think he integrated and drew the graph with a numerical algorithm.
Note that the graph has 3 possible values for $y$ at $x=-0.1$.
That doesn't sound like a simple function of $x$ does it?

Anyway, if the hitch point travels along the x-axis, the known solution is (see Tractrix on MathWorld)
$$x=L \arsech \frac y L -\sqrt{L^2-y^2}$$
Finding a rotated form of this is bound to be horrible.

Alternatively, we have the parametrized version:
$$\begin{cases}x(t)=L(t-\tanh t) \\ y(t)=L \sech t\end{cases}$$
We can rotate and shift this as desired.
Let me skip the steps for now and jump to the result:
$$\begin{cases}X(t)=x_{e,0} + \frac L{\sqrt{1+m^2}}({(t-\tanh t) - m \sech t})\\
Y(t)=y_{e,0} + \frac L{\sqrt{1+m^2}}({m(t-\tanh t) + \sech t})\end{cases}$$
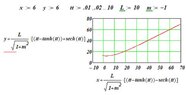
In your case we have approximately $(x_{e,0},y_{e,0})=(6,6)$, $m=1$, and $L=10$.
If we fill that in, we get the following graph from Wolfram|Alpha:

View attachment 8557

Looks the same as yours doesn't it?

 

[Dr Edward]

Wow
Thank you very much
Edward

 

[Dr Edward]

Sorry to trouble you again.
I graphed your equations and got the same result as you. (exciting for me).
Then I played with the coefficients and could not get the position I am looking for.
Here's the MathCad result with different numbers.View attachment 8558
What am i doing wrong?
Here's where I want to be:View attachment 8559
Hope you can help.
Edward

 

[I like Serena]

Looks like $m=-1$ was not substituted correctly...

 

[I like Serena]

Here's what it should look like for $m=-0.1$ ($5.8^\circ$ downwards):
View attachment 8561
Link to graph on W|A.

 

[Dr Edward]

Nice curves - thank you very much.
I have to add a value (shown at the red dot in the picture) to align the cusp to P(0,5).
Also when I change the slope the cusp needs adjustment.
Any idea why this should be?
View attachment 8562
Once again, thanks for bringing me this far.
Edward

 

[Dr Edward]

Hello Klaas,
Hate to be a nuisance but I had a thought.
Is it possible that the sloped hitch line has a y-intercept?
That might explain why the tractrix cusp does not stay on the y-axis.
Would love an answer. A solution? Even better.
Thanks for your input so far.
Edward

 

[I like Serena]

We rotate the graph around the initial hitch end point $(x_{e,0},y_{e,0})$.
So that point always remains the same, and the sloping hitch line intersects it.
The cusp rotates around it just like everything else.

The location of the cusp is $\left(\frac{mL}{\sqrt{1+m^2}}, \frac{L}{\sqrt{1+m^2}}\right)$.
To keep it in the same spot at $(x_{cusp},y_{cusp})$ we can use:
\begin{cases}X(t)=x_{cusp} + \frac L{\sqrt{1+m^2}}({(t-\tanh t) - m(\sech t - 1)})\\
Y(t)=y_{cusp} + \frac L{\sqrt{1+m^2}}({m(t-\tanh t) + (\sech t} - 1))\end{cases}

If we pick $(x_{cusp},y_{cusp})=(0,L)$, the cusp will stay at $(0,L)$.

 

[Dr Edward]

Thanks Heaps.
Works beautifully
Edward