Transfer function of the state space model

[zoom1]

I have a state space model along with an observer and state feedback.

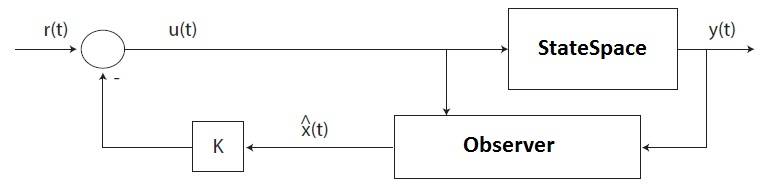
I need to find the transfer function connecting the r (reference) to the y (output)

I have this model on simulink. I know the A,B,C,D matrices. So, I can get the TF for the stateSpace with ss2tf function of matlab. However, I couldn't find a way to obtain the TF of the observer.

Actually I am interested in the poles and zeros of the system. I though if I find the TF, I can get them. But if there is another way around for this, I would also welcome this method.

Thanks

 

[donpacino]

ok, so first what is the equation for a state observer?

 

[zoom1]

ok, so first what is the equation for a state observer?

x_head' = (A-LC)x_head + Bu + Ly

Where x_head is the estimated state array

 

[donpacino]

right...

So use that equation to get the transfer function.

so your A,B,C,D matrixs are the same in the observer as they are in the regular model (at least typically they are)
You should have chosen your L matrix (measurement vs model accuracy).

remember the observer is a MIMO system (multi input multi output)
so to find y/r there is no one simple command, you will have to be smart about how you use matlabas for any easy of finding the poles i'll give you this hint...in the regular state space model X'=AX+Bu
with direct state feedback, the new model is

X'=AX+B(u-KX)

X'=(A-BK)X+Bu

The old poles of the system were the eigenvalues of A. The new poles are the eigenvalues of A-BK
__________________________________________

knowing that, is there an easy way to find the poles of the observer