Trigonometric substitution, a case I'd like to share

[mcastillo356]

TL;DR

There are some steps I haven't got a clue, and some others I should have, but ain't.

Hi, PF
First I will quote it; next the doubts and my attempt:

"In mathematics, trigonometric substitution is the replacement of trigonometric functions for other expresions. In calculus, trigonometric substitution is a technique for evaluating integrals. (...)
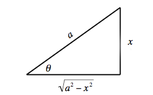
Case I: Integrands containing $a^2-x^2$
Let $x=a\sin\theta$, and use the identity $1-\sin^2\theta=\cos^2\theta$
(...)
Example 1
In the integral
$\displaystyle\int{\displaystyle\frac{dx}{\sqrt{a^2-x^2}}}$
we may use
$x=a\sin\theta,\quad{dx=a\cos\theta\,d\theta,\quad{\theta=\arcsin{\displaystyle\frac{x}{a}}}}$
Then,
$\displaystyle\int{\displaystyle\frac{dx}{\sqrt{a^2-x^2}}}=\displaystyle\int{\displaystyle\frac{a\cos\theta\,d\theta}{\sqrt{a^2-a^2\sin^2\theta}}}$
$\qquad{=\displaystyle\int{\displaystyle\frac{a\cos\theta\,d\theta}{\sqrt{a^2(1-\sin^2\theta)}}}}$
$\qquad{=\displaystyle\frac{a\cos\theta\,d\theta}{\displaystyle\sqrt{a^2\cos^2\theta}}}$
$\qquad{=\displaystyle\int{d\theta}}$
$\qquad{=\theta+C}$
$\qquad{=\arcsin{\displaystyle\frac{x}{a}}+C}$
The above step requires that $a>0$ and $\cos\theta>0$. We can choose a to be the principal root of $a^2$, and impose the restriction $-\pi/2<\theta\<\pi/2$ by using the inverse sine function." (Source: Wikipedia, "Trigonometric substitution".)

Doubts:
(i)- $dx=a\cos\theta\,d\theta$: how is it derived?; any relationship with the Chain Rule?.
(ii)- It is required $a>0$ and $\cos\theta>0$; every nonnegative real number has a unique nonnegative square root, called the principal square root or simply the square root. Am I right?:
(iii)- $-1\leq x\leq 1$ and $-\pi/2\leq y\leq$ are the domain and the range of $y=\arcsin{(x)}$. I've plotted it, etc; should I explore $x=\arcsin{(y)}$? It's clear that $y=\cos{(x)}$ is positive at the first and fourth quadrants.
Well, as you can see, I've put together doubts and attempt.
Greetings!

 

[PeroK]

(i)- $dx=a\cos\theta\,d\theta$: how is it derived?; any relationship with the Chain Rule?.

$$x = a\sin \theta \ \Rightarrow \ \frac{dx}{d\theta} = a\cos \theta \ \Rightarrow \ dx = (a\cos \theta)\ d\theta$$

(ii)- It is required $a>0$ and $\cos\theta>0$; every nonnegative real number has a unique nonnegative square root, called the principal square root or simply the square root. Am I right?:

Technically, you could use $|a| = \sqrt a^2$ in your solution. However, you might as well assume $a > 0$, given that you have only $a^2$ in the original integral.

(iii)- $-1\leq x\leq 1$ and $-\pi/2\leq y\leq$ are the domain and the range of $y=\arcsin{(x)}$. I've plotted it, etc; should I explore $x=\arcsin{(y)}$? It's clear that $y=\cos{(x)}$ is positive at the first and fourth quadrants.
Well, as you can see, I've put together doubts and attempt.
Greetings!
View attachment 331790

In the original integral (assuming $a > 0$), we have $-a \le x \le a$. Hence $-1 \le \frac x a \le 1$. This puts $\frac x a$ within the domain of $\arcsin$. The range of $\arcsin$ is $[-\frac \pi 2, \frac \pi 2]$ and $\cos$ is non-negative on that range.

 

[mcastillo356]

Hi, PF, PeroK

x = a\sin \theta \ \Rightarrow \ \frac{dx}{d\theta} = a\cos \theta \ \Rightarrow \ dx = (a\cos \theta)\ d\theta

No chain rule. It is just the first derivative of $x$ with respect to $\theta$, in the Leibniz notation.

Technically, you could use $|a| = \sqrt a^2$ in your solution. However, you might as well assume $a > 0$, given that you have only $a^2$ in the original integral.

Personally, I prefer the second choice. I keep in mind the concept of $a$ as the principal root of $a^2$: there must be a transition from $a$ squared to $a>0$.

In the original integral (assuming $a > 0$), we have $-a \le x \le a$. Hence $-1 \le \frac a x \le 1$. This puts $\frac a x$ within the domain of $\arcsin$. The range of $\arcsin$ is $[-\frac \pi 2, \frac \pi 2]$ and $\cos$ is non-negative on that range.

Shouldn't it be $\frac x a$?
PD: Post without preview.

 

[PeroK]

Shouldn't it be $\frac x a$?

Yes, fixed.