Trigonometry - Horizon Related Word Problem

[nmnna]

Homework Statement

Persons A and B are at the beach, their eyes are 5 ft and 6 ft, respectively, above sea level. How
many miles farther out is Person B’s horizon than Person A’s?

Relevant Equations

;;

Hello!
I'm trying to solve this problem.
Here's the diagram I tried to make.

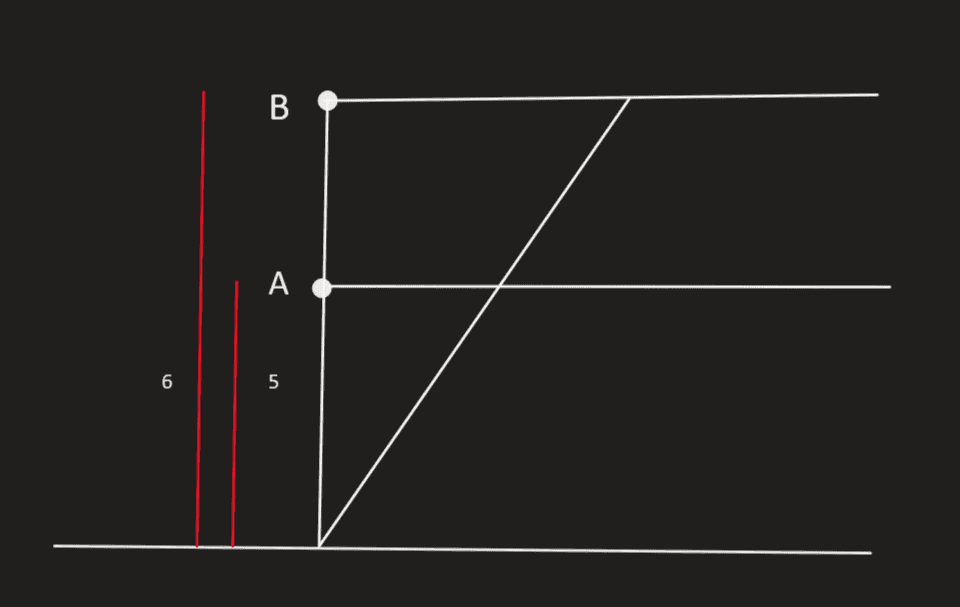
I have difficulty understanding this math problem.. I've tried to solve the problem using the symmetry of the triangles but I didn't get the right answer, and I can't seem to understand the "concept" of the horizon here.
So I'll be grateful if you give me some hints.

 

[Charles Link]

If I'm not mistaken, it is necessary to consider the curvature of the earth, which can be considered to be a sphere with a radius of 4000 miles.

 

[Office_Shredder]

Yeah, I think your diagram is at least very misleading. You have them looking at like, the side of a mountain or something, which isn't really how the horizon works.

 

[phyzguy]

You should view it like this. Line BC is of length R, where R is the radius of the Earth. Line AC is of length R+H, where H is the height of the person. Line AB is tangent to the Earth, so line AB is perpendicular to line BC. You want to calculate the distance AB, which is how far the person is seeing. Remember that H<<R, and use approximations.

 

[Lnewqban]

... but I didn't get the right answer, and I can't seem to understand the "concept" of the horizon here.
So I'll be grateful if you give me some hints.

Welcome, nmnna!
Did they give you a value of radius to use for this problem?

Please, see:
https://en.m.wikipedia.org/wiki/Earth_radius

As explained above, horizon is where the line of sight of a person hits the interface sky-ocean.
That makes that line of sight a line that is simultaneously tangent to the surface of the ocean (at the horizon) and perpendicular to a line from the horizon to the center of the Earth.

Besides the Pythagorean theorem, you could use the tangent-secant theorem, making the secant line go through the center of the Earth:
https://en.m.wikipedia.org/wiki/Tangent-secant_theorem