FairyChatMan
- 9
- 0
Truss Analysis :(
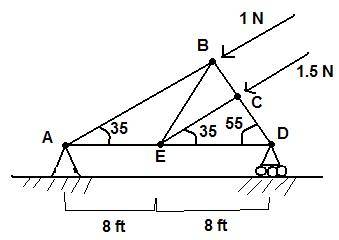
Find the force on each of the members and tell if it is tension of compression.
M = fd \sumFx and Fy = 0
Well, my professor said to us that the first thing to do is to compute for the reactions on the pin. After that, start using Free body diagram on one of the pin, and continue to complete the truss.
Here's what I did...
I set point D as pivot... then
\sumM = 8A - 16cos55 - 12cos55 = 0
A = 2.0075 N upward
But shouldn't the summation of all forces be zero? By having A = 2.0075 and an unknown Rxn on D (which obviously will point upward), the system won't be in equilibrium because cos35 + 1.5cos35 = 2.0479 N.
Just help me getting the correct Reactions on point A and D and i'll be able to solve this problem.. thanks..
=================================
Homework Statement
Find the force on each of the members and tell if it is tension of compression.
Homework Equations
M = fd \sumFx and Fy = 0
The Attempt at a Solution
Well, my professor said to us that the first thing to do is to compute for the reactions on the pin. After that, start using Free body diagram on one of the pin, and continue to complete the truss.
Here's what I did...
I set point D as pivot... then
\sumM = 8A - 16cos55 - 12cos55 = 0
A = 2.0075 N upward
But shouldn't the summation of all forces be zero? By having A = 2.0075 and an unknown Rxn on D (which obviously will point upward), the system won't be in equilibrium because cos35 + 1.5cos35 = 2.0479 N.
Just help me getting the correct Reactions on point A and D and i'll be able to solve this problem.. thanks..
=================================