fishspawned
- 66
- 16
Homework Statement
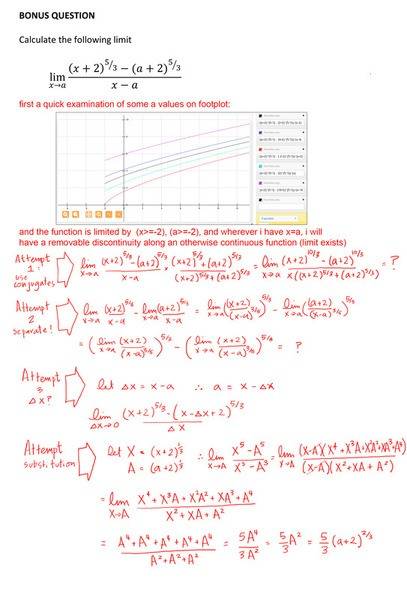
the limit x->a of [(x+2)^5/3 - (a+2)^5/3] / (x-a)
Homework Equations
limit laws
The limit as x approaches a of the expression [(x+2)^(5/3) - (a+2)^(5/3)] / (x-a) can be evaluated using limit laws without direct differentiation. The discussion highlights the challenges posed by the fractional exponent of 5/3, which complicates expansion. A suggested approach involves substituting y = x + 2 and using the limit transformation to simplify the expression to lim_{X→A}[(X^5 - A^5)/(X^3 - A^3)]. This method effectively resolves the 0/0 indeterminate form and leads to the correct limit result.
PREREQUISITESStudents studying calculus, particularly those focusing on limits and derivatives, as well as educators seeking to clarify concepts related to fractional powers and limit evaluation techniques.
Correct result.fishspawned said:DELTA:
this seems to take care of it - provided you know how to expand a sum of powers to a high level - had to look it up to be honest:
so revised sheet: